题目内容
1. 如图所示,一轻质弹簧下端固定,直立于水平地面上,将质量为m的物体A从离弹簧顶端正上方h高处由静止释放,当物体A下降到最低点P时,其速度变为零,此时弹簧的压缩量为x;若将质量为3m的物体B从离弹簧顶端正上方同一h高处,由静止释放,当物体B也下降到P处时,其速度为( )
如图所示,一轻质弹簧下端固定,直立于水平地面上,将质量为m的物体A从离弹簧顶端正上方h高处由静止释放,当物体A下降到最低点P时,其速度变为零,此时弹簧的压缩量为x;若将质量为3m的物体B从离弹簧顶端正上方同一h高处,由静止释放,当物体B也下降到P处时,其速度为( )| A. | 2$\sqrt{\frac{g(h+x)}{3}}$ | B. | 2$\sqrt{g(h+x)}$ | C. | 2$\sqrt{gh}$ | D. | 2$\sqrt{\frac{gh}{3}}$ |
分析 当物体A下降到最低点P时物体和弹簧组成的系统机械能守恒,对两种情况,分别运用机械能守恒定律列式,抓住到达P处时弹性势能相等求解.
解答 解:设物体到达P处时,弹簧的弹性势能为Ep.
第一种情况:当质量为m的物体从离弹簧顶端正上方h高处下落至P处的过程,由系统的机械能守恒得:mg(h+x)=Ep ①
第二种情况:当质量为3m的物体从离弹簧顶端正上方h高处下落至P处的过程,由系统的机械能守恒得:3mg(h+x)=$\frac{1}{2}•3m{v}^{2}$+Ep ②
①②联立得:v=2$\sqrt{\frac{g(h+x)}{3}}$
故选:B
点评 解决本题的关键要搞清物体下落过中能量转化关系:重力势能一部分转化为物体的动能,另一部分转化为弹簧的弹性势能,还要知道同一弹簧压缩量相同时,则弹性势能就相同;再结合动能定理即可轻松求解.

练习册系列答案
相关题目
9.一物体从长为L的光滑斜面的顶端由静止开始匀加速滑下,经时间t滑到底端,则下列说法正确的是( )
| A. | 物体运动到底端时的速度是$\frac{L}{t}$ | |
| B. | 物体在斜面上运动的中间时刻的即时速度是$\frac{L}{2t}$ | |
| C. | 物体运动到斜面中点时瞬时速度是$\frac{\sqrt{2}L}{t}$ | |
| D. | 物体从顶点运动到斜面中点所需的时间是$\frac{\sqrt{2}t}{4}$ |
16.万有引力定律的表达式为:F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$,其中G为引力常量.把它应用于太阳-行星系统,已知地球绕太阳公转的半径为R,周期为T,则由此可以求出( )
| A. | 地球的质量 | B. | 地球的密度 | C. | 太阳的质量 | D. | 太阳的态度 |
6.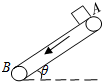 如图所示为粮袋的传送装置,已知AB间长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力)( )
如图所示为粮袋的传送装置,已知AB间长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力)( )
 如图所示为粮袋的传送装置,已知AB间长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力)( )
如图所示为粮袋的传送装置,已知AB间长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力)( )| A. | 粮袋到达B点的速度与v比较,可能比v大,也可能与v相等或比v小 | |
| B. | 粮袋开始运动的加速度为g(sinθ-cosθ),若L足够大,则以后将一定以速度v做匀速运动 | |
| C. | 若μ≤tanθ,则粮袋从A到B一定一直是做加速运动 | |
| D. | 不论μ多大,粮袋从A到B一直匀加速运动,且a>gsinθ |
13.关于点电荷的下列说法中正确的是( )
| A. | 点电荷在自然界是真实存在的 | |
| B. | 点电荷是一种理想模型 | |
| C. | 足够小(如体积小于1mm3)的电荷,就是点电荷 | |
| D. | 一个带电体能否看成点电荷,不是看它的尺寸大小,而是看它的形状和大小对所研究问题的影响是否可忽略不计 |
10. 如图所示,“嫦娥一号”探月卫星被月球捕获后,首先稳定在椭圆轨道Ⅰ上运动,其中P、Q两点分别是轨道Ⅰ的近月点和远月点,Ⅱ是卫星绕月做圆周运动的轨道,轨道Ⅰ和Ⅱ在P点相切,则( )
如图所示,“嫦娥一号”探月卫星被月球捕获后,首先稳定在椭圆轨道Ⅰ上运动,其中P、Q两点分别是轨道Ⅰ的近月点和远月点,Ⅱ是卫星绕月做圆周运动的轨道,轨道Ⅰ和Ⅱ在P点相切,则( )
 如图所示,“嫦娥一号”探月卫星被月球捕获后,首先稳定在椭圆轨道Ⅰ上运动,其中P、Q两点分别是轨道Ⅰ的近月点和远月点,Ⅱ是卫星绕月做圆周运动的轨道,轨道Ⅰ和Ⅱ在P点相切,则( )
如图所示,“嫦娥一号”探月卫星被月球捕获后,首先稳定在椭圆轨道Ⅰ上运动,其中P、Q两点分别是轨道Ⅰ的近月点和远月点,Ⅱ是卫星绕月做圆周运动的轨道,轨道Ⅰ和Ⅱ在P点相切,则( )| A. | 卫星在轨道Ⅰ上运动,P点的速度大于Q点的速度 | |
| B. | 卫星在轨道Ⅰ上运动,P点的加速度小于Q点的加速度 | |
| C. | 卫星沿轨道Ⅰ运动到P点时的加速度大于沿轨道Ⅱ运动到P点时的加速度 | |
| D. | 卫星要从轨道Ⅰ进入轨道Ⅱ,需在P点加速 |
11.物体由静止开始做匀加速直线运动,经过加速8s后,立即做匀减速直线运动,再经过4s停下.关于该物体的运动情况,下列说法正确的是( )
| A. | 加速、减速中的加速度大小之比为 2:1 | |
| B. | 加速、减速中的平均速度大小之比为 2:1 | |
| C. | 加速、减速中的位移大小之比为 2:1 | |
| D. | 加速、减速中的速度的变化率大小之比为 2:1 |
 如图所示,粗糙的水平面与竖直平面内的光滑弯曲轨道BC在B点相接.一小物块从AB上的D点以初速v0=8m/s出发向B点滑行,到达B点时的速度为v=4 m/,物块与水平面间动摩擦因数μ=0.2,求:
如图所示,粗糙的水平面与竖直平面内的光滑弯曲轨道BC在B点相接.一小物块从AB上的D点以初速v0=8m/s出发向B点滑行,到达B点时的速度为v=4 m/,物块与水平面间动摩擦因数μ=0.2,求: