题目内容
7. 如图所示,质量M=20kg的物体从光滑曲面上高度H=0.8m处释放,到达底端时水平进入水平传送带,传送带由一电动机驱动着匀速向左转动,速率为3m/s.已知物体与传送带间的动摩擦因数0.1.(g取10m/s2).求:
如图所示,质量M=20kg的物体从光滑曲面上高度H=0.8m处释放,到达底端时水平进入水平传送带,传送带由一电动机驱动着匀速向左转动,速率为3m/s.已知物体与传送带间的动摩擦因数0.1.(g取10m/s2).求:(1)若两皮带轮之间的距离是10m,物体冲上传送带后就移走光滑曲面,物体将从哪一边离开传送带?通过计算说明你的结论.
(2)若皮带轮间的距离足够大,从M滑上到离开传送带的整个过程中,由于M和传送带间的摩擦而产生了多少热量?
分析 (1)由机械能守恒定律可求得物体滑到曲面底部时的速度,再由动能定理求出物体的速度减至零时在传送带上滑行的距离,再进行判断;
(2)热量等于摩擦力与相对位移间的乘积,由运动学公式求得相对位移,由Q=Fs可求得热量.
解答 解:(1)物体从曲面上下滑时机械能守恒,有 mgH=$\frac{1}{2}$mv02
解得物体滑到曲面底端时的速度 v0=$\sqrt{2gH}$=$\sqrt{2×10×0.8}$m/s=4m/s
以地面为参照系,物体滑上传送带后先向右做匀减速运动,设其速度减至零时向右运动的位移为x.由动能定理得
-μmgs=0-$\frac{1}{2}$mv02
解得 s=8m<10m
之后在传送带的带动下物体将传送带左端离开.
(2)物体运动的加速度大小为 a=$\frac{μmg}{m}$=μg=0.1×10=1m/s2;
物体滑上传送带后向右做匀减速运动的时间为t,则t=$\frac{{v}_{0}}{a}$=$\frac{4}{1}$=4s
这段时间内皮带向左运动的位移大小为 s1=vt=3×4m=12m
物体相对于传送带滑行的距离为△S1=s1+s=8+12=20m
物体与传送带间产生的热量为 Q1=μMg•△S1=0.1×200×20=400J;
物体向左运动的过程中,根据对称性知,若物体向左一直做匀加速运动,回到传送带左端时速度将为4m/s,大于3m/s,不可能,所以物体向左匀加速的末速度等于传送带的速度,设向左匀加速运动的时间为t′.则
t′=$\frac{v}{a}$=$\frac{3}{1}$=3s
这段时间内物体相对于传送带滑行的距离为△S2=vt′-$\frac{vt′}{2}$=$\frac{vt′}{2}$=$\frac{3×3}{2}$m=4.5m
物体与传送带间产生的热量为 Q2=μMg•△S2=0.1×200×4.5=90J;
所以产生的总热量为 Q=Q1+Q2=490J
答:(1)若两皮带轮之间的距离是10m,物体将从左边离开传送带;
(2)M和传送带间的摩擦而产生的热量为490J.
点评 传送带类题目的关键要分析物体的运动过程,要注意摩擦产生的热量为摩擦力与相对位移间的乘积,运用牛顿第二定律和运动学公式结合分析.

 阅读快车系列答案
阅读快车系列答案 滑雪是一项危险性高二技巧性强的运动,某次滑雪过程可近似模拟为两个圆形轨道的对接,如图所示.质量为m的运动员在轨道最低点A的速度为v,且刚好到达最高点B,两圆形轨道的半径相等,均为R,滑雪板与雪面间的摩擦不可忽略,下列说法正确的是( )
滑雪是一项危险性高二技巧性强的运动,某次滑雪过程可近似模拟为两个圆形轨道的对接,如图所示.质量为m的运动员在轨道最低点A的速度为v,且刚好到达最高点B,两圆形轨道的半径相等,均为R,滑雪板与雪面间的摩擦不可忽略,下列说法正确的是( )| A. | 运动员在最高点B时,对轨道的压力为零 | |
| B. | 由A到B过程中增加的重力势能为2mgR-$\frac{1}{2}$mv2 | |
| C. | 由A到B过程中阻力做功为2mgR-$\frac{1}{2}$mv2 | |
| D. | 由A到B过程中损失的机械能为$\frac{1}{2}$mv2 |
| A. | 卫星运行的加速度大小为$\frac{8{π}^{2}R}{{T}^{2}}$ | |
| B. | 该星球的第一宇宙速度大小为$\frac{2πR}{T}$ | |
| C. | 该星球表面的重力加速度大小为$\frac{108{π}^{2}R}{{T}^{2}}$ | |
| D. | 该星球的密度为$\frac{81π}{GT}$ |
 如图,一个原来不带电的半径为r的空心金属球放在绝缘支架上,右侧放置一个电荷量为+Q的点电荷,点电荷到金属球表面的最近距离为2r,下列说法正确的是( )
如图,一个原来不带电的半径为r的空心金属球放在绝缘支架上,右侧放置一个电荷量为+Q的点电荷,点电荷到金属球表面的最近距离为2r,下列说法正确的是( )| A. | 金属球右侧感应出正电荷 | |
| B. | 感应起电后金属球总带电量为-Q | |
| C. | 金属球上的感应电荷在球心处激发的电场强度大小为k$\frac{Q}{9{r}^{2}}$ | |
| D. | 点电荷受到的库仑力大小为k$\frac{{Q}^{2}}{4{r}^{2}}$ |
 如图,粗细均匀、横截面积为S、内壁光滑、竖直放置的玻璃管下端密封,上端封闭但留有一抽气孔.管内下部被活塞封住一定量的热力学温度为T0的理想气体.开始时,活塞上方气体压强为p0,气柱长度为3L,活塞下方气柱长度为L,现将活塞上方抽成真空并密封,抽气过程中管内气体温度始终保持不变.活塞稳定时距玻璃管顶端的距离为L,求:
如图,粗细均匀、横截面积为S、内壁光滑、竖直放置的玻璃管下端密封,上端封闭但留有一抽气孔.管内下部被活塞封住一定量的热力学温度为T0的理想气体.开始时,活塞上方气体压强为p0,气柱长度为3L,活塞下方气柱长度为L,现将活塞上方抽成真空并密封,抽气过程中管内气体温度始终保持不变.活塞稳定时距玻璃管顶端的距离为L,求: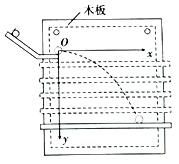 某同学在用如图的装置做“研究平抛物体运动”的实验,已知重力加速度为g,请按要求完成下列填空.
某同学在用如图的装置做“研究平抛物体运动”的实验,已知重力加速度为g,请按要求完成下列填空. 如图所示,质量为M的物体位于倾角为45°的固定光滑斜面上,设对物体施加一个水平向右的恒力,其大小和物体所受的重力的大小相等,则物体的加速度a=0m/s2.
如图所示,质量为M的物体位于倾角为45°的固定光滑斜面上,设对物体施加一个水平向右的恒力,其大小和物体所受的重力的大小相等,则物体的加速度a=0m/s2.