题目内容
17. 如图9所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左轮的半径为3r.c点在左轮上,到左轮中心的距离为r.a点和b点分别位于右轮和左轮的边缘上.若在传动过程中,皮带不打滑.则a、b、c三点的线速度大小之比为3:3:1; a、b、c三点的加速度大小之比为9:3:1.
如图9所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左轮的半径为3r.c点在左轮上,到左轮中心的距离为r.a点和b点分别位于右轮和左轮的边缘上.若在传动过程中,皮带不打滑.则a、b、c三点的线速度大小之比为3:3:1; a、b、c三点的加速度大小之比为9:3:1.
分析 两轮子靠传送带传动,轮子边缘上的点具有相同的线速度,共轴转动的点,具有相同的角速度.j结合v=ωr即可求出线速度之间的关系;
根据a=$\frac{{v}^{2}}{r}$=rω2求出向心加速度的比值.
解答 解:a、b两点是轮子边缘上的点,靠传送带传动,两点的线速度相等.
b、c两点共轴转动,具有相同的角速度;由v=ωr,结合左轮b的半径为3r.c点到左轮中心的距离为r,所以vb:vc=3:1;
所以:va:vb:vc=3:3:1.
a、b两点线速度相等,根据a=$\frac{{v}^{2}}{r}$,知a、b两点的向心加速度之比为3:1.
b、c两点的角速度相等,根据a=rω2,知b、c两点的向心加速度之比为3:1.
所以:aa:ab:ac=9:3:1.
故答案为:3:3:1,9:3:1
点评 解决本题的关键知道靠传送带传动轮子边缘上的点具有相同的线速度,共轴转动的点,具有相同的角速度.以及掌握向心加速度的公式a=$\frac{{v}^{2}}{r}$=rω2.

练习册系列答案
相关题目
8.如图所示,虚线和实线分别为甲、乙两个单摆做简谐运动的图象,则( )


| A. | 甲、乙两个单摆的振幅分别为2cm、1cm | |
| B. | 甲、乙两个单摆的机械能可能相等 | |
| C. | 前2秒内甲乙两个摆球的加速度均为正值 | |
| D. | 第2秒末甲的速度达到最大,乙的回复加速度达到最大 |
2. 如图所示,在竖直墙壁的A点处有一根水平轻杆a,杆的左端有一个轻滑轮O、一根细线上端固定在该天花板的B处,细线跨过滑轮O,下端系一个重为G的物体,开始时BO段细线与天花板的夹角为θ=30°.系统保持静止,轻杆a缓慢向下平移的过程中,不计一切摩擦,下列说法中正确的是( )
如图所示,在竖直墙壁的A点处有一根水平轻杆a,杆的左端有一个轻滑轮O、一根细线上端固定在该天花板的B处,细线跨过滑轮O,下端系一个重为G的物体,开始时BO段细线与天花板的夹角为θ=30°.系统保持静止,轻杆a缓慢向下平移的过程中,不计一切摩擦,下列说法中正确的是( )
 如图所示,在竖直墙壁的A点处有一根水平轻杆a,杆的左端有一个轻滑轮O、一根细线上端固定在该天花板的B处,细线跨过滑轮O,下端系一个重为G的物体,开始时BO段细线与天花板的夹角为θ=30°.系统保持静止,轻杆a缓慢向下平移的过程中,不计一切摩擦,下列说法中正确的是( )
如图所示,在竖直墙壁的A点处有一根水平轻杆a,杆的左端有一个轻滑轮O、一根细线上端固定在该天花板的B处,细线跨过滑轮O,下端系一个重为G的物体,开始时BO段细线与天花板的夹角为θ=30°.系统保持静止,轻杆a缓慢向下平移的过程中,不计一切摩擦,下列说法中正确的是( )| A. | 细线BO对天花板的拉力变大 | |
| B. | a杆对滑轮的作用力逐渐减小 | |
| C. | a杆对滑轮的作用力的方向沿杆水平向右 | |
| D. | 墙壁对a杆的作用力不变 |
9. 某同学利用一段长电阻丝测定一节干电池电动势和内阻.接好如图的实验装置后,将导线的接头O分别连接上电阻丝的a、b、c、d四位置并闭合电路测量.
某同学利用一段长电阻丝测定一节干电池电动势和内阻.接好如图的实验装置后,将导线的接头O分别连接上电阻丝的a、b、c、d四位置并闭合电路测量.
(1)以图示的实验装置为准,a、b、c、d四位置选在从电阻丝左端开始而不是右端的理由是:防止短路,保护电源;
(2)实验中得到两电表读数如表格:
经检查,电阻丝某处发生断路.则根据表格,发生断路的位置在bc(填写字母)两点之间,电源内阻为1.0Ω.
(3)该同学使用的是均匀电阻丝且abcd四点等间距,在不修复电阻丝的情况下,O与电阻丝任意位置连接,不可能出现的电表读数是B
A.1.15V B.1.40V C.0.23A D.0.33A.
 某同学利用一段长电阻丝测定一节干电池电动势和内阻.接好如图的实验装置后,将导线的接头O分别连接上电阻丝的a、b、c、d四位置并闭合电路测量.
某同学利用一段长电阻丝测定一节干电池电动势和内阻.接好如图的实验装置后,将导线的接头O分别连接上电阻丝的a、b、c、d四位置并闭合电路测量.| 接线柱 | a | b | c | d |
| 电压/V | 1.50 | 1.50 | 1.25 | 1.20 |
| 电流/A | 0.00 | 0.00 | 0.25 | 0.30 |
(2)实验中得到两电表读数如表格:
经检查,电阻丝某处发生断路.则根据表格,发生断路的位置在bc(填写字母)两点之间,电源内阻为1.0Ω.
(3)该同学使用的是均匀电阻丝且abcd四点等间距,在不修复电阻丝的情况下,O与电阻丝任意位置连接,不可能出现的电表读数是B
A.1.15V B.1.40V C.0.23A D.0.33A.
6.在相等的时间内动量的变化一定相等的运动有( )
| A. | 匀速圆周运动 | B. | 自由落体运动 | C. | 变速直线运动 | D. | 平抛物体运动 |
 如图所示的平面直角坐标系xOy中,ABCD矩形区域内有磁感应强度为B0的匀强磁场(OD边上无磁场,OA边上有磁场),其中A、D两点的坐标分别为(0,a)和(0,-a),B、C两点的坐标分别为($\sqrt{3}$a,a)和($\sqrt{3}$a,-a);在半径为a、圆心坐标为(-a,0)的圆形区域内有磁感应强度为2B0的匀强磁场,两个区域内磁场方向均垂直纸面向里.在-a≤x≤0的区域均匀分布有大量质量为m、带电荷量为-q的粒子,粒子均以相同的速度沿y轴正方向射向圆形磁场,最后粒子都进入矩形磁场,已知朝着圆心(-a,0)射入的粒子刚好从O点沿x轴正方向进入矩形磁场.不计粒子的重力及粒子间的相互作用.求:
如图所示的平面直角坐标系xOy中,ABCD矩形区域内有磁感应强度为B0的匀强磁场(OD边上无磁场,OA边上有磁场),其中A、D两点的坐标分别为(0,a)和(0,-a),B、C两点的坐标分别为($\sqrt{3}$a,a)和($\sqrt{3}$a,-a);在半径为a、圆心坐标为(-a,0)的圆形区域内有磁感应强度为2B0的匀强磁场,两个区域内磁场方向均垂直纸面向里.在-a≤x≤0的区域均匀分布有大量质量为m、带电荷量为-q的粒子,粒子均以相同的速度沿y轴正方向射向圆形磁场,最后粒子都进入矩形磁场,已知朝着圆心(-a,0)射入的粒子刚好从O点沿x轴正方向进入矩形磁场.不计粒子的重力及粒子间的相互作用.求: ”形的光滑长直导轨槽,槽口向上(图为俯视图).槽内放置一个木质滑块,滑块的左半部是半径为R的半圆柱形光滑凹槽,木质滑块的宽度为2R,比“
”形的光滑长直导轨槽,槽口向上(图为俯视图).槽内放置一个木质滑块,滑块的左半部是半径为R的半圆柱形光滑凹槽,木质滑块的宽度为2R,比“ ”形槽的宽度略小.现有半径r(r<<R)的金属小球以水平初速度V0冲向滑块,从滑块的一侧半圆形槽口边缘进入.已知金属小球的质量为m,木质滑块的质量为3m,整个运动过程中无机械能损失.当金属小球滑离木质滑块时,金属小球和木质滑块的速度各是多大?
”形槽的宽度略小.现有半径r(r<<R)的金属小球以水平初速度V0冲向滑块,从滑块的一侧半圆形槽口边缘进入.已知金属小球的质量为m,木质滑块的质量为3m,整个运动过程中无机械能损失.当金属小球滑离木质滑块时,金属小球和木质滑块的速度各是多大?

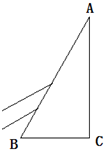 如图所示,一束宽为$\frac{L}{12}$的平行可见光,包含有两种色光,从空气射入顶角为30度的直角透明砖,砖底边长为L,若透明砖对其中一种色光的折射率的折射率n1=$\sqrt{3}$,对另一种色光的折射率为n2<$\sqrt{3}$,当色光上部从AB面中点以60度入射角入射,使这两种色光恰能在透明砖AC表面处射出时分开,则折射率n2至少应为多少?(结果可用反三角函数表示)
如图所示,一束宽为$\frac{L}{12}$的平行可见光,包含有两种色光,从空气射入顶角为30度的直角透明砖,砖底边长为L,若透明砖对其中一种色光的折射率的折射率n1=$\sqrt{3}$,对另一种色光的折射率为n2<$\sqrt{3}$,当色光上部从AB面中点以60度入射角入射,使这两种色光恰能在透明砖AC表面处射出时分开,则折射率n2至少应为多少?(结果可用反三角函数表示)