��Ŀ����
3��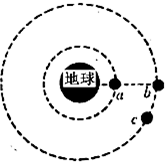 ���й�����Ƽ����Ź�˾��Ժ�������Ƶĵ��ƽ�ϵ��2015��1��2��ȡ����Ҫ�ɹ������ƽ�ϵͳ����������ͻ��6000Сʱ�����ػ�3000�Σ��߱�ȷ���������ڹ�ɿ�����15�����������ͼ��ʾΪӦ�ø�ϵͳ����������a��b��c�Ƶ���������Բ���˶���ʾ��ͼ������b��c���ڰ뾶Ϊr�Ĺ���ϣ�a�ǵ���ͬ�����ǣ���ʱa��bǡ������������֪��������ΪM���뾶ΪR��������ת�Ľ��ٶ�Ϊ�أ�������������ΪG��������
���й�����Ƽ����Ź�˾��Ժ�������Ƶĵ��ƽ�ϵ��2015��1��2��ȡ����Ҫ�ɹ������ƽ�ϵͳ����������ͻ��6000Сʱ�����ػ�3000�Σ��߱�ȷ���������ڹ�ɿ�����15�����������ͼ��ʾΪӦ�ø�ϵͳ����������a��b��c�Ƶ���������Բ���˶���ʾ��ͼ������b��c���ڰ뾶Ϊr�Ĺ���ϣ�a�ǵ���ͬ�����ǣ���ʱa��bǡ������������֪��������ΪM���뾶ΪR��������ת�Ľ��ٶ�Ϊ�أ�������������ΪG��������| A�� | ����b������С��24Сʱ | |
| B�� | ����b��c�Ļ�е����� | |
| C�� | ������a��b��һ�������������辭��ʱ��t=$\frac{2��}{{��-\sqrt{\frac{GM}{r^3}}}}$ | |
| D�� | ����a�Ķ��ܽϴ� |
���� �����Ƶ���Բ���˶��������������������ṩ���ݴ��ɰ뾶��ϵ�������ڴ�С�����ٶȹ�ϵ�������ٴ���������������ת���ĽǶȲ�Ϊ2�У��ɴ˷������㼴�ɣ�
��� �⣺A���������������ṩ������������$G\frac{mM}{{r}^{2}}=mr��\frac{2��}{T}��^{2}$�ɵ���������T=$\sqrt{\frac{4{��}^{2}{r}^{3}}{G{T}^{2}}}$���ɴ˿�֪���ǹ���뾶Խ����������Խ������aΪͬ�����ǣ�������b�����ڴ���ͬ�����ǵ����ڼ�24h����A����
B�����ǵĻ�е�ܵ����䶯��������֮�ͣ���֪�����ǵ��������ʲ���ȷ�����ǵĻ�е�ܴ�С��ϵ����B����
C���������������ṩ��������$G\frac{mM}{{r}^{2}}=mr{��}^{2}$���ɵ�b���ǵĽ��ٶ�$��=\sqrt{\frac{GM}{{r}^{3}}}$����֪�뾶Խ����ٶ�ԽС�����������������ٴ�������ʱ��Բ���˶�ת���ĽǶȲ�Ϊ2�У����Կɵþ�����ʱ��$t=\frac{2��}{��-\sqrt{\frac{GM}{{r}^{3}}}}$����C��ȷ��
D���������������ṩ��������$G\frac{mM}{{r}^{2}}=m\frac{{v}^{2}}{r}$���ɵ����ǵĶ���${E}_{k}=\frac{1}{2}m{v}^{2}=\frac{1}{2}•\frac{GmM}{r}$�����ܵĴ�С�����ǵ�����Ҳ�йأ���δ֪���������Ĵ�С���ʲ���ȷ�����Ƕ��ܵĴ�С����D����
��ѡ��C��
���� ����������Ĵ�������Ҫץס����Բ���˶��������������������ṩ���ܸ������ǹ���뾶�Ĵ�Сȷ����������Բ���˶��������Ĵ�С�ǽ������Ĺؼ���

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| A�� | ��������ʱ��abcd���и�Ӧ���� | |
| B�� | �������Сʱ��abcd���и�Ӧ���� | |
| C�� | ���費�䣬��abcd����ԭ�����ڵ�ƽ������PQ����ʱ�������и�Ӧ���� | |
| D�� | ���費�䣬��abcd����ԭ�����ڵ�ƽ������ֱ�����˶�ʱ�������и�Ӧ���� |
| A�� | �仯���ɲ�ͬ�����ʲ�ͬ | B�� | �仯������ͬ��������ͬ | ||
| C�� | �仯���ɲ�ͬ��������ͬ | D�� | �仯������ͬ�����ʲ�ͬ |
| A�� | ������Բ���˶����������ܵ���������С���䣬��һ������ | |
| B�� | ��Բ���˶������壬�����ļ��ٶ�һ��ָ��Բ�� | |
| C�� | ������תʱ�������ϸ�������ļ��ٶȶ�ָ����� | |
| D�� | ������ֻ�ı������ٶȵķ����ı������ٶȵĴ�С |
 ��ͼ��ʾ��P��ˮƽ���õ��㹻���Բ�̣��ƾ���Բ��O�����ֱ������ת������Բ���Ϸ��̶���ˮƽ�ּ��ϣ�����ʢˮСͰ�Ļ��ִ���СͰһ����v=0.1m/s���ٶ����������˶���СͰ�ײ���Բ���ϱ���ĸ߶Ȳ�Ϊh=5m��t=0ʱ��СͰ�˶���O�����Ϸ��ҵγ���һ��ˮ���Ժ�ÿ��һ��ˮ�պ�����Բ����ʱͰ��ǡ���ٵγ�һ��ˮ�����ƿ�����������Ҫʹˮ�ζ�����Բ���ϵ�ͬһ��ֱ���ϣ�Բ�̽��ٶȵ���СֵΪ�أ����=��rad/s���ڶ�������ˮ����������Ϊd����d=0.5m��
��ͼ��ʾ��P��ˮƽ���õ��㹻���Բ�̣��ƾ���Բ��O�����ֱ������ת������Բ���Ϸ��̶���ˮƽ�ּ��ϣ�����ʢˮСͰ�Ļ��ִ���СͰһ����v=0.1m/s���ٶ����������˶���СͰ�ײ���Բ���ϱ���ĸ߶Ȳ�Ϊh=5m��t=0ʱ��СͰ�˶���O�����Ϸ��ҵγ���һ��ˮ���Ժ�ÿ��һ��ˮ�պ�����Բ����ʱͰ��ǡ���ٵγ�һ��ˮ�����ƿ�����������Ҫʹˮ�ζ�����Բ���ϵ�ͬһ��ֱ���ϣ�Բ�̽��ٶȵ���СֵΪ�أ����=��rad/s���ڶ�������ˮ����������Ϊd����d=0.5m��


