题目内容
9.登月火箭关闭发动机后再离月球表面112km的空中沿圆形轨道运动,周期为120.5min,月球的半径是1740km,根据这些数据计算月球的质量和平均密度(G=6.67×10-11N•m2/kg2)分析 登月舱所受月球的万有引力提供其圆周运动的向心力,根据万有引力定律和向心力公式求出月球质量,再由质量与体积之比求出密度.
解答 解:设登月舱的质量为m,轨道半径为r,月球的半径为R,质量为M.对于登月舱,根据万有引力等于向心力,则得:
$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}r}{{T}^{2}}$
解得:M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}=\frac{4×3.14×[(112+1740)×1{0}^{3}]^{3}}{6.67×1{0}^{-11}×(120.5×60)^{2}}$kg=7.2×1022kg
月球的平均密度为:ρ=$\frac{M}{V}=\frac{7.2×1{0}^{22}}{\frac{4}{3}×3.14×(1740×1{0}^{3})^{3}}$kg/m3=2.7×103 kg/m3.
答:月球的质量为7.2×1022kg,平均密度为2.7×103 kg/m3.
点评 本题属于已知环绕天体的轨道半径和周期,求解中心天体质量的类型,建立模型,利用万有引力等于向心力这一基本思路进行求解.

练习册系列答案
相关题目
19. 如图所示,光滑斜面的顶端固定一弹簧,一物体向右滑行,并冲上固定在地面上的斜面.设物体在斜面最低点A的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中克服弹簧的弹力做功为( )
如图所示,光滑斜面的顶端固定一弹簧,一物体向右滑行,并冲上固定在地面上的斜面.设物体在斜面最低点A的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中克服弹簧的弹力做功为( )
 如图所示,光滑斜面的顶端固定一弹簧,一物体向右滑行,并冲上固定在地面上的斜面.设物体在斜面最低点A的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中克服弹簧的弹力做功为( )
如图所示,光滑斜面的顶端固定一弹簧,一物体向右滑行,并冲上固定在地面上的斜面.设物体在斜面最低点A的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中克服弹簧的弹力做功为( )| A. | mgh-$\frac{1}{2}$mv2 | B. | $\frac{1}{2}$mv2-mgh | C. | -mgh | D. | -(mgh+$\frac{1}{2}$mv2) |
12. 如图,金属棒ab置于水平放置的U形光滑导轨上,在ef右侧存在有界匀强磁场B,磁场方向垂直导轨平面向下,在ef左侧的无磁场区域cdef内有一半径很小的金属圆环L,圆环与导轨在同一平面内.当金属棒ab在水平恒力F作用下从磁场左边界ef处由静止开始向右运动后,对圆环L,下列说法正确的是( )
如图,金属棒ab置于水平放置的U形光滑导轨上,在ef右侧存在有界匀强磁场B,磁场方向垂直导轨平面向下,在ef左侧的无磁场区域cdef内有一半径很小的金属圆环L,圆环与导轨在同一平面内.当金属棒ab在水平恒力F作用下从磁场左边界ef处由静止开始向右运动后,对圆环L,下列说法正确的是( )
 如图,金属棒ab置于水平放置的U形光滑导轨上,在ef右侧存在有界匀强磁场B,磁场方向垂直导轨平面向下,在ef左侧的无磁场区域cdef内有一半径很小的金属圆环L,圆环与导轨在同一平面内.当金属棒ab在水平恒力F作用下从磁场左边界ef处由静止开始向右运动后,对圆环L,下列说法正确的是( )
如图,金属棒ab置于水平放置的U形光滑导轨上,在ef右侧存在有界匀强磁场B,磁场方向垂直导轨平面向下,在ef左侧的无磁场区域cdef内有一半径很小的金属圆环L,圆环与导轨在同一平面内.当金属棒ab在水平恒力F作用下从磁场左边界ef处由静止开始向右运动后,对圆环L,下列说法正确的是( )| A. | 圆环L有收缩趋势,圆环内的感应电流变小 | |
| B. | 圆环L有扩张趋势,圆环内的感应电流变大 | |
| C. | 圆环L有收缩趋势,圆环内的感应电流不变 | |
| D. | 圆环L有扩张趋势,圆环内的感应电流变小 |
13. 如图所示为汽车在水平路面上启动过程中的v-t图象,汽车在行驶过程中所受阻力恒为F阻,Oa段为过原点的倾斜直线,ab段表示以额定功率行驶时的加速阶段,bc段是与ab段相切的水平直线,则下述说法中正确的是( )
如图所示为汽车在水平路面上启动过程中的v-t图象,汽车在行驶过程中所受阻力恒为F阻,Oa段为过原点的倾斜直线,ab段表示以额定功率行驶时的加速阶段,bc段是与ab段相切的水平直线,则下述说法中正确的是( )
 如图所示为汽车在水平路面上启动过程中的v-t图象,汽车在行驶过程中所受阻力恒为F阻,Oa段为过原点的倾斜直线,ab段表示以额定功率行驶时的加速阶段,bc段是与ab段相切的水平直线,则下述说法中正确的是( )
如图所示为汽车在水平路面上启动过程中的v-t图象,汽车在行驶过程中所受阻力恒为F阻,Oa段为过原点的倾斜直线,ab段表示以额定功率行驶时的加速阶段,bc段是与ab段相切的水平直线,则下述说法中正确的是( )| A. | 0~t1时间内汽车做匀加速运动且功率恒定 | |
| B. | 0~t1时间内汽车牵引力做功为$\frac{{F}_{阻}{v}_{1}}{2{t}_{1}}$ | |
| C. | t1~t2时间内的平均速度为$\frac{1}{2}$(v1+v2) | |
| D. | 在全过程中t1时刻的牵引力及功率都是最大值,t2~t3时间内牵引力最小 |
 如图所示,质量m1=0.3kg 的小车静止在光滑的水平面上,车长L=15m,现有质量m2=0.2kg可视为质点的物块,以水平向右的速度v0=2m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.5,取g=10m/s2,求:
如图所示,质量m1=0.3kg 的小车静止在光滑的水平面上,车长L=15m,现有质量m2=0.2kg可视为质点的物块,以水平向右的速度v0=2m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.5,取g=10m/s2,求: 如图所示,两个底面积都是S的圆筒,用一根带阀门的很细的管子相连接,放在水平面上,两桶内装有密度为ρ的同种液体,阀门关闭时两桶液面的高度分别为h1和h2,现将连接两桶的阀门打开,在两桶液面变成相同高度的过程中重力做了多少功?
如图所示,两个底面积都是S的圆筒,用一根带阀门的很细的管子相连接,放在水平面上,两桶内装有密度为ρ的同种液体,阀门关闭时两桶液面的高度分别为h1和h2,现将连接两桶的阀门打开,在两桶液面变成相同高度的过程中重力做了多少功?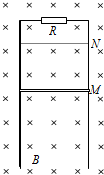 如图所示,在磁感应强度为B的水平匀强磁场中,有一竖直放置的光滑金属导轨,导轨平面与磁场垂直,导轨间距为L,顶端接有阻值为R的电阻,将一根金属棒从导轨上的M处以速度v0竖直向上抛出,棒到达N处后返回,回到出发点M时棒的速度为抛出时的一半.已知棒的长度为L,质量为m,电阻为r.金属棒始终在磁场中运动,处于水平且与导轨接触良好,忽略导轨的电阻.重力加速度为g.
如图所示,在磁感应强度为B的水平匀强磁场中,有一竖直放置的光滑金属导轨,导轨平面与磁场垂直,导轨间距为L,顶端接有阻值为R的电阻,将一根金属棒从导轨上的M处以速度v0竖直向上抛出,棒到达N处后返回,回到出发点M时棒的速度为抛出时的一半.已知棒的长度为L,质量为m,电阻为r.金属棒始终在磁场中运动,处于水平且与导轨接触良好,忽略导轨的电阻.重力加速度为g. 一长为2L的轻杆,一端固定一个质量为m的小球A,另一端固定一个质量为2m的小球B,中点处固定一转动轴O.轻杆可绕固定轴O在竖直面内自由转动.现将杆置于水平位置,如图所示,然后静止释放,不计各处摩擦与空气阻力,求:
一长为2L的轻杆,一端固定一个质量为m的小球A,另一端固定一个质量为2m的小球B,中点处固定一转动轴O.轻杆可绕固定轴O在竖直面内自由转动.现将杆置于水平位置,如图所示,然后静止释放,不计各处摩擦与空气阻力,求: