题目内容
19. 如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则( )
如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则( )| A. | b的周期小于c的周期 | |
| B. | b、c周期相等,且大于a的周期 | |
| C. | b的向心力大于c的向心力 | |
| D. | b、c的线速度大小相等,且小于a的线速度 |
分析 根据万有引力提供向心力,得出线速度、加速度、周期与轨道半径的大小关系,从而比较出大小.
解答 解:A、根据万有引力提供向心力得:
F=$\frac{GMm}{{r}^{2}}$=$\frac{{{m4π}^{2}r}^{\;}}{{T}^{2}}$=m$\frac{{v}^{2}}{r}$
A、T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,轨道半径越大,周期越大.所以b、c的周期相同,大于a的周期.故A错误,B正确;
C、根据F=$\frac{GMm}{{r}^{2}}$,因为a、b质量相同,且小于c的质量,而bc半径相同大于a的半径,所以Fa>Fb,Fc>Fb,可知b所需向心力最小.故C错误;
D、v=$\sqrt{\frac{GM}{r}}$,轨道半径越大,线速度越小,所以b、c的线速度相等,小于a的线速度.故D正确.
故选:BD.
点评 本题关键抓住万有引力提供向心力,先列式求解出线速度、周期和加速度的表达式,再进行讨论.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
9. 如图所示,两根细线挂着两个质量相同的小球A和B,原来两个小球都不带电,现让它们带上电量相同的异种电荷,则正确的是( )
如图所示,两根细线挂着两个质量相同的小球A和B,原来两个小球都不带电,现让它们带上电量相同的异种电荷,则正确的是( )
 如图所示,两根细线挂着两个质量相同的小球A和B,原来两个小球都不带电,现让它们带上电量相同的异种电荷,则正确的是( )
如图所示,两根细线挂着两个质量相同的小球A和B,原来两个小球都不带电,现让它们带上电量相同的异种电荷,则正确的是( )| A. | 上面绳子受到的拉力增大 | B. | 上面绳子受到的拉力不变 | ||
| C. | 下面绳子受到的拉力减小; | D. | 下面绳子受到的拉力不变 |
10. 如图为一台理想变压器,初、次级线圈的匝数分别为n1=400匝,n2=800匝.连接导线的电阻忽略不计,那么可以确定( )
如图为一台理想变压器,初、次级线圈的匝数分别为n1=400匝,n2=800匝.连接导线的电阻忽略不计,那么可以确定( )
 如图为一台理想变压器,初、次级线圈的匝数分别为n1=400匝,n2=800匝.连接导线的电阻忽略不计,那么可以确定( )
如图为一台理想变压器,初、次级线圈的匝数分别为n1=400匝,n2=800匝.连接导线的电阻忽略不计,那么可以确定( )| A. | 这是一台升压变压器 | |
| B. | 次级线圈两端的电压是初级线圈两端电压的一半 | |
| C. | 通过次级线圈的电流是通过初级线圈电流的一半 | |
| D. | 变压器输出的电功率是输入的电功率的一半 |
7.某同学在百米赛跑中,测得他在50m处的瞬时速度为8m/s,12.5s末到达终点的瞬时速度为10m/s,则他在全程内的平均速度是( )
| A. | 6m/s | B. | 8m/s | C. | 9m/s | D. | 10m/s |
4.某物体运动的v-t图象如图所示,根据图象可知( )


| A. | 0时刻的加速度大小为0 | |
| B. | 0~5s内的位移为14m | |
| C. | 第1s末与第4.5s末的加速度方向相反 | |
| D. | 第1s末与第4.5s末的速度方向相反 |
8.一辆农用“小四轮”漏油,假如每隔l s漏下一滴,车在平直公路上行驶,一位同学根据漏在路面上的油滴分布,分析“小四轮”的运动情况(已知车的运动方向).下列说法中正确的是( )
| A. | 当沿运动方向油滴间距逐渐增大时,小四轮做加速直线运动 | |
| B. | 当沿运动方向油滴始终均匀分布时,小四轮做匀速直线运动 | |
| C. | 当沿运动方向油滴间距逐渐增大时,车的加速度可能在减小 | |
| D. | 当沿运动方向油滴间距逐渐增大时,车的加速度可能在增大 |

 如图所示,A、B两物体叠放在水平地面上,已知A、B的质量分别为mA=10kg,mB=20kg,A、B之间以及B与地面之间的动摩擦因数均为μ=0.5,一轻绳一端系住物体A,另一端系于墙上,绳与竖直方向的夹角为37°,今欲用外力将物体B匀速向右拉出,求:水平力F的大小.(已知sin37°=0.6,cos37°=0.8)
如图所示,A、B两物体叠放在水平地面上,已知A、B的质量分别为mA=10kg,mB=20kg,A、B之间以及B与地面之间的动摩擦因数均为μ=0.5,一轻绳一端系住物体A,另一端系于墙上,绳与竖直方向的夹角为37°,今欲用外力将物体B匀速向右拉出,求:水平力F的大小.(已知sin37°=0.6,cos37°=0.8)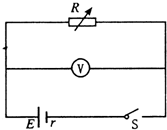 如图所示,R为电阻箱,V为理想电压表.当电阻箱读数为R1=2Ω时,电压表读数为 U1=3V;当电阻箱读数为R2=4Ω时,电压表读数为U2=4V.求:
如图所示,R为电阻箱,V为理想电压表.当电阻箱读数为R1=2Ω时,电压表读数为 U1=3V;当电阻箱读数为R2=4Ω时,电压表读数为U2=4V.求: