题目内容
9. 在做“研究匀变速直线运动”的实验时,某同学得到一条用打点计时器打下的纸带,如图所示,并在其上取了A、B、C、D、E、F等6个计数点,(每相邻两个计数点间还有4个打点计时器打下的点,本图中没有画出)打点计时器接的是“220V、50Hz”的交变电流.如图1,他把一把毫米刻度尺放在纸带上,其零刻度和计数点A对齐,求:
在做“研究匀变速直线运动”的实验时,某同学得到一条用打点计时器打下的纸带,如图所示,并在其上取了A、B、C、D、E、F等6个计数点,(每相邻两个计数点间还有4个打点计时器打下的点,本图中没有画出)打点计时器接的是“220V、50Hz”的交变电流.如图1,他把一把毫米刻度尺放在纸带上,其零刻度和计数点A对齐,求:(1)打点计时器在打D点时物体的瞬时速度vD=0.21m/s,打点计时器在打B、C、E各点时物体的瞬时速度如下表:
| vB | vC | vD | vE |
| 0.12m/s | 0.16m/s | 0.25m/s |
(3)如果当时电网中交变电流的频率是f=49Hz,而做实验的同学并不知道,那么由此引起的系统误差将使加速度的测量值比实际值偏大.
分析 (1)根据某段时间内的平均速度等于中间时刻的瞬时速度求出D点的瞬时速度.
(2)作出v-t图线,结合图线的斜率求出物体的加速度.
(3)根据周期的测量误差,通过加速度的表达式得出加速度的测量误差.
解答  解:(1)每相邻两个计数点间还有4个打点计时器打下的点,即相邻两个计数点的时间间隔是0.1s
解:(1)每相邻两个计数点间还有4个打点计时器打下的点,即相邻两个计数点的时间间隔是0.1s
根据匀变速直线运动中时间中点的瞬时速度等于该过程中的平均速度,则有:
${v}_{D}=\frac{{x}_{CE}}{2T}=\frac{0.0650-0.0240}{0.2}$m/s=0.21m/s
(2)先描点,再连线,画出直线,如图:
在直线上取相距较远的两点,读出坐标,求出斜率为:
k=$\frac{0.24-0.12}{0.3}=0.40m/{s}^{2}$.
则加速度大小为0.40m/s2.
(3)根据△x=aT2知,a=$\frac{△x}{{T}^{2}}$,由于周期的测量值偏小,则加速度的测量值偏大,所以测量值比实际值偏大.
故答案为:(1)0.21;(2)图象如图,0.40;(3)大.
点评 解决本题的关键掌握纸带的处理方法,会通过纸带求解瞬时速度和加速度,以及知道速度时间的斜率表示加速度,难度不大.

练习册系列答案
相关题目
20.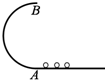 如图所示,半径为R的光滑半圆形轨道和光滑水平轨道相切,三个小球1、2、3沿水平轨道分别以速度v1=2$\sqrt{gR}$、v2=3$\sqrt{gR}$、v3=4$\sqrt{gR}$水平向左冲上半圆形轨道,g为重力加速度,下列关于三个小球的落点到半圆形轨道最低点A的水平距离和离开轨道后的运动形式的说法正确的是( )
如图所示,半径为R的光滑半圆形轨道和光滑水平轨道相切,三个小球1、2、3沿水平轨道分别以速度v1=2$\sqrt{gR}$、v2=3$\sqrt{gR}$、v3=4$\sqrt{gR}$水平向左冲上半圆形轨道,g为重力加速度,下列关于三个小球的落点到半圆形轨道最低点A的水平距离和离开轨道后的运动形式的说法正确的是( )
 如图所示,半径为R的光滑半圆形轨道和光滑水平轨道相切,三个小球1、2、3沿水平轨道分别以速度v1=2$\sqrt{gR}$、v2=3$\sqrt{gR}$、v3=4$\sqrt{gR}$水平向左冲上半圆形轨道,g为重力加速度,下列关于三个小球的落点到半圆形轨道最低点A的水平距离和离开轨道后的运动形式的说法正确的是( )
如图所示,半径为R的光滑半圆形轨道和光滑水平轨道相切,三个小球1、2、3沿水平轨道分别以速度v1=2$\sqrt{gR}$、v2=3$\sqrt{gR}$、v3=4$\sqrt{gR}$水平向左冲上半圆形轨道,g为重力加速度,下列关于三个小球的落点到半圆形轨道最低点A的水平距离和离开轨道后的运动形式的说法正确的是( )| A. | 三个小球离开轨道后均做平抛运动 | |
| B. | 小球2和小球3的落点到A点的距离之比为$\sqrt{5}$:2$\sqrt{3}$ | |
| C. | 小球1和小球2做平抛运动的时间之比为1:1 | |
| D. | 小球2和小球3做平抛运动的时间之比为1:1 |
17.一质点自t=0时从静止开始做直线运动,其速度随时间变化如图所示.下列选项正确的是( )


| A. | 在0~6s内,物体离出发点最远为30m | |
| B. | 在0~6s内,物体经过的路程为50m | |
| C. | 在0~4s内,物体的平均速率为7.5m/s | |
| D. | 在4~6s内,物体所受的合外力发生了变化 |
14.下列说法正确的是( )
| A. | 甲分子固定不动,乙分子从很远处向甲靠近到不能再靠近的过程中,分子间的分子力先做正功后做负功 | |
| B. | 当两分子间距离大于平衡位置的间距r0时,随分子间距离增大,引力与斥力都减小,引力减小的更快 | |
| C. | 由于液体表面分子间距离大于液体内部分子间的距离,故液体表面存在表面张力 | |
| D. | 当两分子间距离大于平衡位置的间距r0时,分子间的距离越大,分子势能越大 | |
| E. | 气体很容易充满整个容器,这是分子间存在斥力的宏观表现 |
1.下列说法不符合物理学史的是( )
| A. | 奥斯特发现了电流的磁效应 | |
| B. | 法拉第发现了电磁感应现象 | |
| C. | 布朗观察到了液体分子的运动 | |
| D. | 楞次找到了判断感应电流方向的方法 |
16. 在探究单摆周期与摆长关系的实验中:
在探究单摆周期与摆长关系的实验中:
(1)关于安装仪器及测量时的一些实验操作,下列说法正确的是C.(选填选项前面的字母)
A.用米尺测出摆线的长度,记为摆长l
B.先将摆球和摆线放在水平桌面上测量摆长l,再将单摆悬挂在铁架台上
C.使摆线偏离竖直方向某一角度α(小于10°),然后静止释放摆球
D.测出摆球两次通过最低点的时间间隔记为此单摆振动的周期
(2)实验测得的数据如下表所示.
请将第三次的测量数据标在图中,并在图中作出T2随l变化的关系图象.
(3)根据数据及图象可知单摆周期的平分与摆长的关系是周期的平方与摆长成正比.
(4)根据图象,可求得当地的重力加速度为9.86m/s2.(结果保留3位有效数字)
 在探究单摆周期与摆长关系的实验中:
在探究单摆周期与摆长关系的实验中:(1)关于安装仪器及测量时的一些实验操作,下列说法正确的是C.(选填选项前面的字母)
A.用米尺测出摆线的长度,记为摆长l
B.先将摆球和摆线放在水平桌面上测量摆长l,再将单摆悬挂在铁架台上
C.使摆线偏离竖直方向某一角度α(小于10°),然后静止释放摆球
D.测出摆球两次通过最低点的时间间隔记为此单摆振动的周期
(2)实验测得的数据如下表所示.
| 次数 | 1 | 2 | 3 | 4 | 5 |
| 摆长l/cm | 80.00 | 90.00 | 100.00 | 110.00 | 120.00 |
| 30次全振动时间t/s | 53.8 | 56.9 | 60.0 | 62.8 | 65.7 |
| 振动周期T/s | 1.79 | 1.90 | 2.00 | 2.09 | 2.19 |
| 振动周期的平分T2/s2 | 3.20 | 3.61 | 4.00 | 4.37 | 4.80 |
(3)根据数据及图象可知单摆周期的平分与摆长的关系是周期的平方与摆长成正比.
(4)根据图象,可求得当地的重力加速度为9.86m/s2.(结果保留3位有效数字)


