题目内容
3. 如图所示,A、B两物体通过定滑轮连接,其质量分别为M和m,光滑斜面的倾角为θ,绳的一端连着B,另一端固定在A上.由静止释放,B开始加速向下运动,求:
如图所示,A、B两物体通过定滑轮连接,其质量分别为M和m,光滑斜面的倾角为θ,绳的一端连着B,另一端固定在A上.由静止释放,B开始加速向下运动,求:(1)A、B两物体的加速度大小;
(2)绳中张力大小.
分析 (1)对整体分析,根据牛顿第二定律求出AB一起做匀加速直线运动的加速度大小.
(2)对B物体受力分析,根据牛顿第二定律计算绳中张力的大小.
解答 解:(1)对整体分析,根据牛顿第二定律得:
mg-Mgsinθ=(M+m)a
解得:a=$\frac{mg-Mgsinθ}{(M+m)a}$
(2)对B受力分析可得:mg-F=ma
绳中张力大小为:F=mg-ma=mg-m$\frac{mg-Mgsinθ}{(M+m)a}$
答:(1)A、B两物体的加速度大小为$\frac{mg-Mgsinθ}{(M+m)a}$;
(2)绳中张力大小为mg-m$\frac{mg-Mgsinθ}{(M+m)a}$.
点评 解决本题的关键能够正确地受力分析,运用牛顿第二定律计算加速度的大小,运用整体法和隔离法的计算拉力的大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.2014年诺贝尔物理学奖被授予了日本科学家赤崎勇、天野浩和美籍日裔科学家中村修二,以表彰他们发明蓝色发光二极管(LED),并因此带来新型的节能光源.在物理学的发展过程中,许多物理学家的科学发现推动了人类历史的进步.下列表述符合物理学史实的是( )
| A. | 库仑发现了电流的热效应 | |
| B. | 安培发现了电流的磁效应 | |
| C. | 法拉第发现了磁场产生电流的条件和规律 | |
| D. | 伽利略提出的万有引力定律奠定了天体力学的基础 |
11. 真空中有一静电场,其在x轴正半轴的电势φ随x变化的关系如图所示,则根据图象可知( )
真空中有一静电场,其在x轴正半轴的电势φ随x变化的关系如图所示,则根据图象可知( )
 真空中有一静电场,其在x轴正半轴的电势φ随x变化的关系如图所示,则根据图象可知( )
真空中有一静电场,其在x轴正半轴的电势φ随x变化的关系如图所示,则根据图象可知( )| A. | R处的电场强度E=0 | |
| B. | x1处与x2处的电场强度方向相反 | |
| C. | 若正的试探电荷从x1处移到x2处,电场力一定做正功 | |
| D. | 该电场有可能是处在O点的正的点电荷激发产生的 |
5.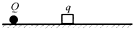 如图所示,在粗糙、绝缘且足够大的水平面上固定着一个带负电荷的点电荷Q.将一个质量为m带电荷为q的小金属块(金属块可以看成为质点)放在水平面上并由静止释放,金属块将在水平面上沿远离Q的方向开始运动.则在金属块运动的整个过程中( )
如图所示,在粗糙、绝缘且足够大的水平面上固定着一个带负电荷的点电荷Q.将一个质量为m带电荷为q的小金属块(金属块可以看成为质点)放在水平面上并由静止释放,金属块将在水平面上沿远离Q的方向开始运动.则在金属块运动的整个过程中( )
 如图所示,在粗糙、绝缘且足够大的水平面上固定着一个带负电荷的点电荷Q.将一个质量为m带电荷为q的小金属块(金属块可以看成为质点)放在水平面上并由静止释放,金属块将在水平面上沿远离Q的方向开始运动.则在金属块运动的整个过程中( )
如图所示,在粗糙、绝缘且足够大的水平面上固定着一个带负电荷的点电荷Q.将一个质量为m带电荷为q的小金属块(金属块可以看成为质点)放在水平面上并由静止释放,金属块将在水平面上沿远离Q的方向开始运动.则在金属块运动的整个过程中( )| A. | 电场力对金属块做的功等于金属块增加的机械能 | |
| B. | 金属块的电势能一直减少 | |
| C. | 金属块的加速度先增大后减小 | |
| D. | 电场对金属块所做的功一定等于摩擦产生的热 |

 如图所示,物体A被压在物体B和水平地面之间,B用绳拴在墙上,物体A和物体B的质量分别为10kg和30kg,物体A与物体B及物体A与地面之间的动摩擦因数均为μ=0.2.若将物体A向右抽出,在抽出过程中,物体A与体B之间的摩擦力为60N,物体A与地面之间的摩擦力为80N.(取g=10N/kg)
如图所示,物体A被压在物体B和水平地面之间,B用绳拴在墙上,物体A和物体B的质量分别为10kg和30kg,物体A与物体B及物体A与地面之间的动摩擦因数均为μ=0.2.若将物体A向右抽出,在抽出过程中,物体A与体B之间的摩擦力为60N,物体A与地面之间的摩擦力为80N.(取g=10N/kg)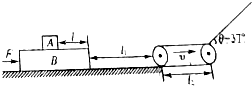 如图所示,在光滑的水平面上有一质量为2m的足够长的长木板B,其上表面离长木板B的右端距离为l=0.7m处放一质量为m的物块A(可视为质点),长木板离传送带左侧的距离为l1=3.2m,且传送带的上端与长木板B的上表面相平齐.现给长木板B一个水平向右,大小为F=$\frac{3}{2}$μmg的推力,当长木板B与传送带左侧相碰的瞬间,长木板B立即停止且固定不动,同时撤去力F,物块A以某一速度滑上以顺时针匀速转动,速度为v(未知)、长度为l2=0.5m的传送带后滑上与水平面夹角为θ=37°的足够长的斜面,且物块A在斜面上上滑过程的位移与时间关系为s=kt-5t2(m)且k>0,已知物块A与长木板B、传送带及斜面之间的动摩擦因数均为μ,传送带转动轮大小忽略不计,滑块A通过轨道衔接处时无能量损失,重力加速度取g=10m/s2.求:(已知sin37°=0.6,cos37°=0.8)
如图所示,在光滑的水平面上有一质量为2m的足够长的长木板B,其上表面离长木板B的右端距离为l=0.7m处放一质量为m的物块A(可视为质点),长木板离传送带左侧的距离为l1=3.2m,且传送带的上端与长木板B的上表面相平齐.现给长木板B一个水平向右,大小为F=$\frac{3}{2}$μmg的推力,当长木板B与传送带左侧相碰的瞬间,长木板B立即停止且固定不动,同时撤去力F,物块A以某一速度滑上以顺时针匀速转动,速度为v(未知)、长度为l2=0.5m的传送带后滑上与水平面夹角为θ=37°的足够长的斜面,且物块A在斜面上上滑过程的位移与时间关系为s=kt-5t2(m)且k>0,已知物块A与长木板B、传送带及斜面之间的动摩擦因数均为μ,传送带转动轮大小忽略不计,滑块A通过轨道衔接处时无能量损失,重力加速度取g=10m/s2.求:(已知sin37°=0.6,cos37°=0.8)