题目内容
12. 如图所示,带等量异种电荷的粒子a,b以相同的速率从O点射入宽度为d的有界匀强磁场,两粒子的入射方向与磁场边界的夹角分别为30°和60°,且同时到达P点(不计粒子的重力),则a、b两粒子的质量之比ma:mb和通过磁场区域的时间之比Ta:Tb( )
如图所示,带等量异种电荷的粒子a,b以相同的速率从O点射入宽度为d的有界匀强磁场,两粒子的入射方向与磁场边界的夹角分别为30°和60°,且同时到达P点(不计粒子的重力),则a、b两粒子的质量之比ma:mb和通过磁场区域的时间之比Ta:Tb( )| A. | ma:mb=1:$\sqrt{3}$ | B. | ma:mb=$\sqrt{3}$:1 | C. | Ta:Tb=$\sqrt{3}$:2 | D. | Ta:Tb=2:$\sqrt{3}$ |
分析 作出粒子的轨迹图,根据几何关系求出两个粒子在磁场中的半径关系,结合半径公式求出两个粒子的质量之比.
解答  解:A、根据题意画出a、b粒子的轨迹如图所示,则a、b粒子的圆心分别是O1和O2,设磁场宽度为d,由图可知,
解:A、根据题意画出a、b粒子的轨迹如图所示,则a、b粒子的圆心分别是O1和O2,设磁场宽度为d,由图可知,
粒子a的半径为:r1=$\frac{\frac{d}{2}}{sin6°}$=$\frac{d}{\sqrt{3}}$,
粒子b的半径为:r2=$\frac{\frac{d}{2}}{sin30°}$=d
根据Bqv=m$\frac{{v}^{2}}{r}$可得:m=$\frac{qmr}{v}$,
因为两粒子速率相等,半径之比为ra:rb=1:$\sqrt{3}$,且电量相等,则两粒子的质量之比为ma:mb=1:$\sqrt{3}$.故A正确,B错误.
C、粒子运动周期T=$\frac{2πm}{Bq}$,则可知周期之比为:1:$\sqrt{3}$;
由图可知,a粒子的圆心角为120°,而b粒子圆心角为60°,则根据t=$\frac{θ}{360}T$可知,两粒子在磁场中运动的时间之比为Ta:Tb=2:$\sqrt{3}$,故C错误,D正确;
故选:AD
点评 本题考查带电粒子在磁场中的运动规律,求解有关带电粒子在有界磁场中的运动问题的关键是画出轨迹图,并根据几何知识确定圆心求出半径和圆心角,再结合圆周运动的有关规律联立即可求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3. 如图所示,理想变压器原、副线圈匝数比为n1:n2=5:3,原线圈接有u=110$\sqrt{2}$sin 100πt(V)的交流电,副线圈电路中a、b、c、d为四个理想二极管,定值电阻R=6Ω,电表皆为理想交流电表,则下列说法中正确的是( )
如图所示,理想变压器原、副线圈匝数比为n1:n2=5:3,原线圈接有u=110$\sqrt{2}$sin 100πt(V)的交流电,副线圈电路中a、b、c、d为四个理想二极管,定值电阻R=6Ω,电表皆为理想交流电表,则下列说法中正确的是( )
 如图所示,理想变压器原、副线圈匝数比为n1:n2=5:3,原线圈接有u=110$\sqrt{2}$sin 100πt(V)的交流电,副线圈电路中a、b、c、d为四个理想二极管,定值电阻R=6Ω,电表皆为理想交流电表,则下列说法中正确的是( )
如图所示,理想变压器原、副线圈匝数比为n1:n2=5:3,原线圈接有u=110$\sqrt{2}$sin 100πt(V)的交流电,副线圈电路中a、b、c、d为四个理想二极管,定值电阻R=6Ω,电表皆为理想交流电表,则下列说法中正确的是( )| A. | 电压表示数为132 V | |
| B. | 电流表示数为3.3 A | |
| C. | 定值电阻R消耗的电功率为363 W | |
| D. | 若把b、d两二极管换成6Ω的定值电阻,则电流表示数为4.4 A |
4. 如图所示,匝数n=100匝、面积为S=0.448m2的导线框ABCD所在处的磁感应强度大小B=$\frac{\sqrt{2}}{10π}$T.线框绕垂直于磁场的轴OO′以角速度ω=100π rad/s匀速转动,并与理想升压变压器相连进行远距离输电,升压变压器的原副线圈匝数比为2:5,理想降压变压器副线圈接入一只“220V 1100W”的灯泡,且灯泡正常发光,输电线路总电阻r=20Ω,导线框及其余导线电阻不计,电表均为理想电表.则下列说法中不正确的是( )
如图所示,匝数n=100匝、面积为S=0.448m2的导线框ABCD所在处的磁感应强度大小B=$\frac{\sqrt{2}}{10π}$T.线框绕垂直于磁场的轴OO′以角速度ω=100π rad/s匀速转动,并与理想升压变压器相连进行远距离输电,升压变压器的原副线圈匝数比为2:5,理想降压变压器副线圈接入一只“220V 1100W”的灯泡,且灯泡正常发光,输电线路总电阻r=20Ω,导线框及其余导线电阻不计,电表均为理想电表.则下列说法中不正确的是( )
 如图所示,匝数n=100匝、面积为S=0.448m2的导线框ABCD所在处的磁感应强度大小B=$\frac{\sqrt{2}}{10π}$T.线框绕垂直于磁场的轴OO′以角速度ω=100π rad/s匀速转动,并与理想升压变压器相连进行远距离输电,升压变压器的原副线圈匝数比为2:5,理想降压变压器副线圈接入一只“220V 1100W”的灯泡,且灯泡正常发光,输电线路总电阻r=20Ω,导线框及其余导线电阻不计,电表均为理想电表.则下列说法中不正确的是( )
如图所示,匝数n=100匝、面积为S=0.448m2的导线框ABCD所在处的磁感应强度大小B=$\frac{\sqrt{2}}{10π}$T.线框绕垂直于磁场的轴OO′以角速度ω=100π rad/s匀速转动,并与理想升压变压器相连进行远距离输电,升压变压器的原副线圈匝数比为2:5,理想降压变压器副线圈接入一只“220V 1100W”的灯泡,且灯泡正常发光,输电线路总电阻r=20Ω,导线框及其余导线电阻不计,电表均为理想电表.则下列说法中不正确的是( )| A. | 电压表的读数为448 V | |
| B. | 输电线路的电流为0.98 A | |
| C. | 电流表的读数为2.5 A | |
| D. | 降压变压器的原副线圈匝数比为5:1 |
17.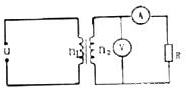 如图所示,理想变压器原线圈的输入电压u=1000$\sqrt{2}$sin200πt(V),变压器副线圈与一个定值电阻R=100Ω相连,变压器原、副线圈的匝数n1:n2=10:1,电压表和电流表均是理想交流表,下列说法正确的是( )
如图所示,理想变压器原线圈的输入电压u=1000$\sqrt{2}$sin200πt(V),变压器副线圈与一个定值电阻R=100Ω相连,变压器原、副线圈的匝数n1:n2=10:1,电压表和电流表均是理想交流表,下列说法正确的是( )
 如图所示,理想变压器原线圈的输入电压u=1000$\sqrt{2}$sin200πt(V),变压器副线圈与一个定值电阻R=100Ω相连,变压器原、副线圈的匝数n1:n2=10:1,电压表和电流表均是理想交流表,下列说法正确的是( )
如图所示,理想变压器原线圈的输入电压u=1000$\sqrt{2}$sin200πt(V),变压器副线圈与一个定值电阻R=100Ω相连,变压器原、副线圈的匝数n1:n2=10:1,电压表和电流表均是理想交流表,下列说法正确的是( )| A. | 输人电压为正弦交变电压,其周期T=O.02s | |
| B. | 电压表的示数为100V,电流表的示数为1OA | |
| C. | 电压表的示数为I00在v,电流表的示数为1O$\sqrt{2}$A | |
| D. | 电阻R消耗的电功率为100W |
4. 如图所示,滑轮A可沿倾角60°的足够长轨道下滑,滑轮下用轻绳挂着一个重力为G的物体B,下滑时,物体B相对于A静止,绳与竖直方向夹角为30°,则下滑过程中(不计空气阻力)( )
如图所示,滑轮A可沿倾角60°的足够长轨道下滑,滑轮下用轻绳挂着一个重力为G的物体B,下滑时,物体B相对于A静止,绳与竖直方向夹角为30°,则下滑过程中(不计空气阻力)( )
 如图所示,滑轮A可沿倾角60°的足够长轨道下滑,滑轮下用轻绳挂着一个重力为G的物体B,下滑时,物体B相对于A静止,绳与竖直方向夹角为30°,则下滑过程中(不计空气阻力)( )
如图所示,滑轮A可沿倾角60°的足够长轨道下滑,滑轮下用轻绳挂着一个重力为G的物体B,下滑时,物体B相对于A静止,绳与竖直方向夹角为30°,则下滑过程中(不计空气阻力)( )| A. | A、B的加速度为gsin60° | B. | A、B的加速度为gsin30° | ||
| C. | 绳的拉力为Gcos30° | D. | 滑轮A与轨道之间一定有摩擦 |
1. 用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,则( )
用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,则( )
 用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,则( )
用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,则( )| A. | 小球所带电荷量为$\frac{b+mg}{E}$ | B. | 轻绳的长度为$\frac{a}{b}$ | ||
| C. | 小球在最高点时的最小速度为$\sqrt{\frac{2a}{m}}$ | D. | 小球在最低点时的最小速度为$\sqrt{\frac{5a}{m}}$ |
2.如图甲,光滑导轨电阻不计,间距为L,固定在倾角为θ的斜面上.区域1内有垂直于斜面的匀强磁场Bx(Bx未知),区域2有垂直于斜面向下的磁场,其大小变化如图乙所示,区域2沿斜面的长度为2L. t=0时在轨道上端由静止释放金属细棒ab,t=tx(tx未知)恰好进入区域2.在ab棒从开始运动至到达EF的过程中,另一金属棒cd始终静止在区域1,已知cd棒的质量为m,重力加速度为g.则( )

| A. | 两棒的质量不相等 | |
| B. | ab棒的机械能先不变后减少 | |
| C. | ab棒从开始运动至到达EF的过程中,克服安培力做功为2mgLsinθ | |
| D. | ab棒从开始运动至到达EF的过程中,回路中产生的焦耳热为4mgLsinθ |

 如图所示,轻绳绕过定滑轮,一端与质量为m的物体相连,另一端受到大小为F的恒力作用,开始时绳与水平方向夹角为α.物体由静止沿水平面从A点被拉到B点,然后沿斜面被拉到滑轮O处.已知AB=BO=L,不计物体与滑轮的大小和滑轮轴的摩擦,在这一过程中恒力F做功为2FLcosα;若物体与水平面间的动摩擦因数为$\frac{\sqrt{3}}{3}$,开始时绳与水平方向夹角α=20°,那么物体在AB段运动时加速度大小的变化情况为先增大后减小.
如图所示,轻绳绕过定滑轮,一端与质量为m的物体相连,另一端受到大小为F的恒力作用,开始时绳与水平方向夹角为α.物体由静止沿水平面从A点被拉到B点,然后沿斜面被拉到滑轮O处.已知AB=BO=L,不计物体与滑轮的大小和滑轮轴的摩擦,在这一过程中恒力F做功为2FLcosα;若物体与水平面间的动摩擦因数为$\frac{\sqrt{3}}{3}$,开始时绳与水平方向夹角α=20°,那么物体在AB段运动时加速度大小的变化情况为先增大后减小.