��Ŀ����
15������ͼ1װ�ÿ�������ѧ�е�����ʵ�飬��1������˵����ȷ����BD��
A���ô�װ�á��о��ȱ���ֱ���˶���ʱ�������跨����С���ͻ�����Ħ��������Ӱ��
B���ô�װ�á��о��ȱ���ֱ���˶���ʱ������������ָ߶�ʹ����С����ϸ���뻬��ƽ��
C���ô�װ�á�̽�����ٶ�a����F�Ĺ�ϵ��ÿ�θı����뼰������������֮����Ҫ����ƽ��Ħ����
D���ô�װ�á�̽�����ٶ�a����F�Ĺ�ϵ��ӦʹС�̺����������������ԶС��С��������
��2�������ô�װ�á�̽�����ٶ�a����F�Ĺ�ϵ��ʱ��ʵ���а��淶���������һ��ֽ����һ������ͼ2����֪����ʱ������Ƶ��Ϊ50Hz�Ľ�����Դ�ϣ���˴�ʵ���д���ʱ������A ��ʱС����˲ʱ�ٶ�Ϊ0.53m/s�����������2λ��Ч���֣�

��3������ͼ1װ�òⶨij�ȱ���ֱ���˶��ļ��ٶȣ����õ���ͼ3ֽ������0�㿪ʼÿ5����ȡһ�������㣬���ڼ������ʱ����ΪT�����մ����Ⱥ�˳�����α��Ϊ1��2��3��4��5��6���������������ľ���ֱ����s1��s2��s3��s4��s5��s6������ȱ���ֱ���˶��ļ��ٶ�a=$\frac{{s}_{4}+{s}_{5}+{s}_{6}-{s}_{1}-{s}_{2}-{s}_{3}}{9{T}^{2}}$��
���� ��1������ͼʾС��ֽ��װ�ÿ�����ɺܶ�ʵ�飬���о��ȱ���ֱ���˶�ʱ����Ҫƽ��Ħ��������̽����С���ļ��ٶ��������Ĺ�ϵ����̽���������ٶȱ仯�Ĺ�ϵ��ʵ��ʱ����Ҫƽ��Ħ��������̽����С���ļ��ٶ�a����F�Ĺ�ϵ��ʱ������ţ�ٵڶ�����������ٶ�a�ı���ʽ�����ѵó������������ԶԶ����С��������ʱ�����ٶ�a���Ƶ���g�Ľ��ۣ�
��2�������м�ʱ�̵��ٶȵ���ƽ���ٶ����A���ٶȣ�
��3�������ȱ���ֱ���˶������ۡ�s=aT2�������������ٶ�a��
��� �⣺��1��A����װ�ÿ��������о��ȱ���ֱ���˶���������Ҫƽ��Ħ��������A����
B���ô�װ�á��о��ȱ���ֱ���˶���ʱ��Ϊ��ʹС�����ȼ���ֱ���˶�������������ָ߶�ʹ����С����ϸ���뻬��ƽ�У���B��ȷ��
C���ô�װ�á�̽�����ٶ�a����F�Ĺ�ϵ��ʱ��ͨ������С���ϵ�����ı�����ʱ������Ҫ���µ���ľ����б�ȣ���C����
D�������ø�װ������̽������ļ��ٶ������������Ĺ�ϵ��ʱ����С��������ΪM��С���̺�������������Ϊm��������������ΪF��
������Ϊ�о�������mg=��m+M��a
���a=$\frac{mg}{M+m}$
��MΪ�о����������ӵ�����F=Ma=$\frac{M}{M+m}$mg
��ȻҪ��F=mg����m+M=M������M����m����ֻ��M����mʱ�ſ�����Ϊ����С����������С����С���̺�����������������D��ȷ��
��ѡ��BD��
��2�������ȱ���ֱ���˶����м�ʱ���ٶȵ������ʱ���ڵ�ƽ���ٶȵã�
vA=$\frac{x}{2T}$=$\frac{21��1{0}^{-2}}{2��0.02}$m/s��0.53m/s
��3���������ã�
s4-s1=3a1T2��s5-s2=3a2T2��s6-s3=3a3T2��
�ȱ���ֱ���˶��ļ��ٶ�Ϊ��a=$\frac{{a}_{1}+{a}_{2}+{a}_{3}}{3}$
�����ã�a=$\frac{{s}_{4}+{s}_{5}+{s}_{6}-{s}_{1}-{s}_{2}-{s}_{3}}{9{T}^{2}}$
�ʴ�Ϊ����1��BD����2��0.53����3��$\frac{{s}_{4}+{s}_{5}+{s}_{6}-{s}_{1}-{s}_{2}-{s}_{3}}{9{T}^{2}}$��
���� ���ʵ����������Ҫ���ո�ʵ��ԭ�����ȱ���ֱ���˶������ۣ��˽�ʵ��IJ�����������ݴ����Լ�ע�����Ȼ������Ӧ���������������ʵ�����⣬֪���ȱ���ֱ���˶��м�ʱ�̵��ٶȵ���ƽ���ٶȣ���ȷ��s=aT2��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д� ��ͼ��ʾ���ô�ϸ������ֱ����ͬ��ͬ�ֽ����������Ƴ������ֱ�Ϊn1��n2����Բ�αպ���ȦA��B����֪����Ȧ�İ뾶֮��Ϊr1��r2�������Ƿ���ͬһ��ǿ�ų��У�����Ȧƽ������ǿ�ų��ĴŸ��ߴ�ֱ�����Ÿ�Ӧǿ����ʱ����ȱ仯ʱ�������ʱ����ͨ������Ȧ����ijһ����ĵ���֮��qA��qBΪ��������
��ͼ��ʾ���ô�ϸ������ֱ����ͬ��ͬ�ֽ����������Ƴ������ֱ�Ϊn1��n2����Բ�αպ���ȦA��B����֪����Ȧ�İ뾶֮��Ϊr1��r2�������Ƿ���ͬһ��ǿ�ų��У�����Ȧƽ������ǿ�ų��ĴŸ��ߴ�ֱ�����Ÿ�Ӧǿ����ʱ����ȱ仯ʱ�������ʱ����ͨ������Ȧ����ijһ����ĵ���֮��qA��qBΪ��������| A�� | $\frac{n_1}{n_2}$ | B�� | $\frac{n_2}{n_1}$ | C�� | $\frac{r_1}{r_2}$ | D�� | $\frac{r_2}{r_1}$ |
| A�� | ��M��Ķ��ܱ���N��С0.2J | B�� | ��M��Ļ�е�ܱ���N���0.1J | ||
| C�� | ��M����������ܱ���N���0.3J | D�� | ��M��ĵ����ܱ���N���0.1J |
| A�� | �����˶��ļ��ٶȵ���0�����ٶ�ȴ������ | |
| B�� | ��������ȣ�һ��������ٶȱ仯�������ٶ�ȴ�Ƚ�С | |
| C�� | ��������ļ��ٶȣ����ٶȵķ���ȴ���� | |
| D�� | ������ֱ���˶�����һ�εļ��ٶȱ�ǰһ��С�����ٶ�ȴ��ǰһ�δ� |
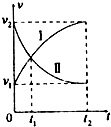 ��ͬһ�ص�ͬʱ��ʼ��ͬһֱ���˶�����������I��II���ٶ�ͼ����ͼ��ʾ����0��t2ʱ���ڣ�����˵������ȷ���ǣ�������
��ͬһ�ص�ͬʱ��ʼ��ͬһֱ���˶�����������I��II���ٶ�ͼ����ͼ��ʾ����0��t2ʱ���ڣ�����˵������ȷ���ǣ�������| A�� | ������������t1ʱ������ | |
| B�� | �����������ƽ���ٶȴ�С����$\frac{{{v_1}+{v_2}}}{2}$ | |
| C�� | �������������ܵĺ��������ڲ��ϼ�С | |
| D�� | ������ļ��ٶȲ�����������ļ��ٶȲ��ϼ�С |

 �ڡ���֤��е���غ㶨�ɡ���ʵ���У�
�ڡ���֤��е���غ㶨�ɡ���ʵ���У� ��ͼ��ʾ��һ������Ϊm�������+q�Ĵ��������������Բ��ƣ����Ӿ�ֹ��ʼ��U1��ѹ���ٺ�ˮƽ������ƽ�н�������ƫת�糡�У������峤L��������d�������ƫת�糡ʱ��ƫת�Ǧ�=30�㣬�ֽ��Ž���һ������ֱ��ֽ���������ǿ�ų�������
��ͼ��ʾ��һ������Ϊm�������+q�Ĵ��������������Բ��ƣ����Ӿ�ֹ��ʼ��U1��ѹ���ٺ�ˮƽ������ƽ�н�������ƫת�糡�У������峤L��������d�������ƫת�糡ʱ��ƫת�Ǧ�=30�㣬�ֽ��Ž���һ������ֱ��ֽ���������ǿ�ų�������