题目内容
16. 甲、乙两球的质量相等,悬线一长一短,将两球由图示位置的同一水平面无初速度释放,不计阻力,则对两小球过最低点时的状态描述正确的是( )
甲、乙两球的质量相等,悬线一长一短,将两球由图示位置的同一水平面无初速度释放,不计阻力,则对两小球过最低点时的状态描述正确的是( )| A. | 两球的角速度大小相等 | |
| B. | 两球的加速度大小相等 | |
| C. | 甲球的动能与乙球的动能相等 | |
| D. | 相对同一参考面,两球的机械能相等 |
分析 A、B两球在运动的过程中,只有重力做功,机械能守恒,比较出初始位置的机械能即可知道在最低点的机械能大小.
根据动能定理mgL=$\frac{1}{2}m{v}^{2}$,可比较出A、B两球的动能大小.
根据动能定理或机械能守恒求出在最低点的速度,然后根据ma=m$\frac{{v}^{2}}{L}$,得出向心加速度的大小关系.
解答 解:A、根据动能定理有:$\frac{1}{2}m{v}^{2}$=mgL
所以:v=$\sqrt{2gL}$
在最低点的角速度:$ω=\frac{v}{L}=\sqrt{\frac{2g}{L}}$.悬线的长度不相等,则两球的角速度不相等.故A错误;
B、在最低点,根据牛顿第二定律得:ma=m$\frac{{v}^{2}}{L}$,
向心加速度为:a=$\frac{{v}^{2}}{L}$=2g,加速度相等,故B正确;
C、根据动能定理$\frac{1}{2}m{v}^{2}$=mgL可知,由于绳长不等,则甲乙两球动能不等.故C错误;
D、A、B两球在运动的过程中,只有重力做功,机械能守恒,初始位置的机械能相等,所以在最低点,两球的机械能相等.故D正确.
故选:BD
点评 解决本题的关键掌握动能定理和机械能守恒定律,知道摆球在最低点靠合力提供做圆周运动的向心力.

练习册系列答案
相关题目
6.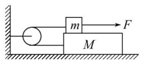 如图所示,木板质量为M,长度为L,小木块(可视为质点)的质量为m,水平地面光滑,一根不计质量的轻绳通过定滑轮分别与木板和小木块连接,小木块与木板间的动摩擦因数为μ,开始时木块静止在木板左端,现用水平向右的力将小木块拉至木板右端,拉力至少做功为( )
如图所示,木板质量为M,长度为L,小木块(可视为质点)的质量为m,水平地面光滑,一根不计质量的轻绳通过定滑轮分别与木板和小木块连接,小木块与木板间的动摩擦因数为μ,开始时木块静止在木板左端,现用水平向右的力将小木块拉至木板右端,拉力至少做功为( )
 如图所示,木板质量为M,长度为L,小木块(可视为质点)的质量为m,水平地面光滑,一根不计质量的轻绳通过定滑轮分别与木板和小木块连接,小木块与木板间的动摩擦因数为μ,开始时木块静止在木板左端,现用水平向右的力将小木块拉至木板右端,拉力至少做功为( )
如图所示,木板质量为M,长度为L,小木块(可视为质点)的质量为m,水平地面光滑,一根不计质量的轻绳通过定滑轮分别与木板和小木块连接,小木块与木板间的动摩擦因数为μ,开始时木块静止在木板左端,现用水平向右的力将小木块拉至木板右端,拉力至少做功为( )| A. | 2μmgL | B. | μmgL | C. | μ(M+m)gL | D. | $\frac{μmgL}{2}$ |
7. 如图所示,一理想变压器的原线圈接有电压为U的交流电,副线圈接有电阻R1、光敏电阻R2(阻值随光照增强而减小),开关K开始时处于闭合状态,下列说法正确的是( )
如图所示,一理想变压器的原线圈接有电压为U的交流电,副线圈接有电阻R1、光敏电阻R2(阻值随光照增强而减小),开关K开始时处于闭合状态,下列说法正确的是( )
 如图所示,一理想变压器的原线圈接有电压为U的交流电,副线圈接有电阻R1、光敏电阻R2(阻值随光照增强而减小),开关K开始时处于闭合状态,下列说法正确的是( )
如图所示,一理想变压器的原线圈接有电压为U的交流电,副线圈接有电阻R1、光敏电阻R2(阻值随光照增强而减小),开关K开始时处于闭合状态,下列说法正确的是( )| A. | 当光照变弱时,变压器的输入功率增加 | |
| B. | 当滑动触头P向下滑动时,电阻R1消耗的功率增加 | |
| C. | 当开关K由闭合到断开,原线圈中电流变大 | |
| D. | 当U增大时,副线圈中电流变小 |
11. 笫56届日本电池大会上华为发布了5分钟即可充满3000mAh电池50%电量的快充技术成果,引起业界广泛关注.如图是华为某智能手机电池上的信息,支持低压大电流充电,则( )
笫56届日本电池大会上华为发布了5分钟即可充满3000mAh电池50%电量的快充技术成果,引起业界广泛关注.如图是华为某智能手机电池上的信息,支持低压大电流充电,则( )
 笫56届日本电池大会上华为发布了5分钟即可充满3000mAh电池50%电量的快充技术成果,引起业界广泛关注.如图是华为某智能手机电池上的信息,支持低压大电流充电,则( )
笫56届日本电池大会上华为发布了5分钟即可充满3000mAh电池50%电量的快充技术成果,引起业界广泛关注.如图是华为某智能手机电池上的信息,支持低压大电流充电,则( )| A. | 4.35V表示该电池的电动势 | |
| B. | 11.4 Wh表示该电池能提供的电量 | |
| C. | 3000 mAh表示该电池能提供的电能 | |
| D. | 该电池充满电后以后以100mA的电流工作时,可连续工作30小时 |
8.下列说法正确的是( )
| A. | 某些原子核能够放射出β粒子,说明原子核内有β粒子 | |
| B. | 核泄漏事故污染物137Cs能够产生对人体有害的辐射,其核反应方程式为55137Cs→56137Ba+X,可以判断X为电子 | |
| C. | 某种色光照射金属发生光电效应,若增大光照强度,则单位时间内发射的光电子数减少 | |
| D. | 若氢原子从n=6能级向n=1能级跃迁时辐射出的光不能使某金属发生光电效应,则氢原子从n=6能级向n=2能级跃迁时辐射出的光能可能使该金属发生光电效应 |
2. 如图所示,一长木板放置在水平面上,可视为质点的小物块放置在长木板的左端,各接触面都是粗糙的.某时刻在物块上施加一水平向右恒力F,使物块与木板一起由静止开始向右作匀加速直线运动且两者保持相对静止,其中长木板和地面之间的最大静摩擦力为F1,小物块与长木板之间的最大静摩擦力为F2,以下说法正确的是( )
如图所示,一长木板放置在水平面上,可视为质点的小物块放置在长木板的左端,各接触面都是粗糙的.某时刻在物块上施加一水平向右恒力F,使物块与木板一起由静止开始向右作匀加速直线运动且两者保持相对静止,其中长木板和地面之间的最大静摩擦力为F1,小物块与长木板之间的最大静摩擦力为F2,以下说法正确的是( )
 如图所示,一长木板放置在水平面上,可视为质点的小物块放置在长木板的左端,各接触面都是粗糙的.某时刻在物块上施加一水平向右恒力F,使物块与木板一起由静止开始向右作匀加速直线运动且两者保持相对静止,其中长木板和地面之间的最大静摩擦力为F1,小物块与长木板之间的最大静摩擦力为F2,以下说法正确的是( )
如图所示,一长木板放置在水平面上,可视为质点的小物块放置在长木板的左端,各接触面都是粗糙的.某时刻在物块上施加一水平向右恒力F,使物块与木板一起由静止开始向右作匀加速直线运动且两者保持相对静止,其中长木板和地面之间的最大静摩擦力为F1,小物块与长木板之间的最大静摩擦力为F2,以下说法正确的是( )| A. | 水平作用力F的大小必须满足:F1<F≤F2(F1<F2) | |
| B. | 水平作用力F的大小必须满足:F<F1或F>F2(F1<F2) | |
| C. | 某时刻撤去F后,两物块一定保持相对静止 | |
| D. | 某时刻撤去F后,两物块一定会相对运动 |
 用一根细线一段系一小球(可视为质点),另一端固定在一光滑锥顶上,如图所示,设小球在水平面内作匀速圆周运动的角速度为ω,线的张力为FT,则FT随ω2变化的图象是图中的( )
用一根细线一段系一小球(可视为质点),另一端固定在一光滑锥顶上,如图所示,设小球在水平面内作匀速圆周运动的角速度为ω,线的张力为FT,则FT随ω2变化的图象是图中的( )



 如图是探究重锤下落过程中“机械能守恒定律”的实验装置.下列实验步骤操作合理的排列顺序是ADBCEF(填写步骤前面的字母)
如图是探究重锤下落过程中“机械能守恒定律”的实验装置.下列实验步骤操作合理的排列顺序是ADBCEF(填写步骤前面的字母)