��Ŀ����
10���ҹ��������ߺš����˺�����л����Բ���ɹ�������Ա��־���״γɹ�ʵʩ�ռ���ջ��ʵ�����ҹ��ռ似����չ���ش��Խ����֪�ɴ��ڵ����Ͽյ�Բ���������ʱ�����ĸ߶�Ϊh������뾶ΪR�����������������ٶ�Ϊg����ɴ���Բ���������ʱ��������| A�� | ����Ա��־�ճ��պ��������˶� | |
| B�� | �ɴ����ٶȴ�СΪv=R$\sqrt{\frac{g}{R+h}}$ | |
| C�� | �ɴ����ٶ�v���һ�����ٶ�v1�Ĵ�С֮��Ϊ$\frac{v}{{v}_{1}}$=$\sqrt{\frac{R}{R+h}}$ | |
| D�� | �ɴ�����һ�ܵ�ʱ��ΪT=$\frac{2�У�R+h��}{R}$$\sqrt{\frac{R+h}{g}}$ |
���� ����Ա���պ���ɴ�������ͬ�����ٶȣ������������ṩ��������Ȼ������Բ���˶����������������ṩ����������������������������������ٶȺ����ڣ��Լ����ٶ����һ�����ٶ�֮�ȣ�
��� �⣺A������Ա���պ���ɴ�������ͬ�����ٶȣ�����$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$��֪ ����Ա��Ȼ������Բ���˶�����A����
B������$G\frac{Mm}{��R+h��^{2}}=m\frac{{v}^{2}}{R+h}$��GM=gR2�ã��ɴ������ٶ�v=$R\sqrt{\frac{g}{R+h}}$����B��ȷ��
C����һ�����ٶ�${v}_{1}=\sqrt{\frac{GM}{{R}^{\;}}}=\sqrt{gR}$����$\frac{v}{{v}_{1}}=\sqrt{\frac{R}{R+h}}$����C��ȷ��
D������$G\frac{Mm}{��R+h��^{2}}=m��R+h��\frac{4{��}^{2}}{{T}^{2}}$��GM=gR2�����T=$\frac{2�У�R+h��}{R}$$\sqrt{\frac{R+h}{g}}$����D��ȷ��
��ѡ��BCD��
���� �������Ĺؼ����������������ɵ�������Ҫ���ۣ�1�����������ṩ��������2������������������������������ã�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
12��һ���������������壬���¶Ȳ���������£��跨ʹ��ѹǿ����������һ���̣�������
| A�� | ������ܶȼ�С | B�� | ������ӵ�ƽ���������� | ||
| C�� | �����������˹� | D�� | ������������������ |
5�� ��ͼ��ʾ�����BCһ�˴��й⻬�Ķ����֣�B�˹̶�����ֱǽ�ϣ�BC��ǽ�洹ֱ������һ��ϵ��ǽ��A�㣬��ͨ������������һ��ϵ������Ϊm�����壬��������ֱǽ�ļн�Ϊ60�㣬����װ�ô��ھ�ֹ״̬���������ٶ�Ϊg�������ж���ȷ���ǣ�������
��ͼ��ʾ�����BCһ�˴��й⻬�Ķ����֣�B�˹̶�����ֱǽ�ϣ�BC��ǽ�洹ֱ������һ��ϵ��ǽ��A�㣬��ͨ������������һ��ϵ������Ϊm�����壬��������ֱǽ�ļн�Ϊ60�㣬����װ�ô��ھ�ֹ״̬���������ٶ�Ϊg�������ж���ȷ���ǣ�������
 ��ͼ��ʾ�����BCһ�˴��й⻬�Ķ����֣�B�˹̶�����ֱǽ�ϣ�BC��ǽ�洹ֱ������һ��ϵ��ǽ��A�㣬��ͨ������������һ��ϵ������Ϊm�����壬��������ֱǽ�ļн�Ϊ60�㣬����װ�ô��ھ�ֹ״̬���������ٶ�Ϊg�������ж���ȷ���ǣ�������
��ͼ��ʾ�����BCһ�˴��й⻬�Ķ����֣�B�˹̶�����ֱǽ�ϣ�BC��ǽ�洹ֱ������һ��ϵ��ǽ��A�㣬��ͨ������������һ��ϵ������Ϊm�����壬��������ֱǽ�ļн�Ϊ60�㣬����װ�ô��ھ�ֹ״̬���������ٶ�Ϊg�������ж���ȷ���ǣ�������| A�� | ���ϵ��������ظˣ���СΪ$\sqrt{3}$mg | B�� | ���ϵ��������ظˣ���СΪmg | ||
| C�� | ���ϵ����������ظˣ���СΪmg | D�� | ���ϵ����������ظˣ���СΪ$\sqrt{3}$mg |
19�������й�˵���У���ȷ���ǣ�������
| A�� | �������ܵı仯�������������ѡ���й� | |
| B�� | ���ܵı仯��������ѡ���й� | |
| C�� | ͬһ������ͬһ����������������ֵ��������ѡ���й� | |
| D�� | �������뷴�����������ľ���ֵ������ȵ� |
20�� ��ͼ��ʾ��������Ϊ1kg��С��a��b���ᵯ��A��B������F�������´���ƽ��״̬������A��B�������ɾ���ϵ����Ϊ5N/cm��B�����϶����컨��̶����ӣ���������ֱ����ļн�Ϊ60�㣬A������ֱ��gȡ10m/s2��������˵����ȷ���ǣ�������
��ͼ��ʾ��������Ϊ1kg��С��a��b���ᵯ��A��B������F�������´���ƽ��״̬������A��B�������ɾ���ϵ����Ϊ5N/cm��B�����϶����컨��̶����ӣ���������ֱ����ļн�Ϊ60�㣬A������ֱ��gȡ10m/s2��������˵����ȷ���ǣ�������
 ��ͼ��ʾ��������Ϊ1kg��С��a��b���ᵯ��A��B������F�������´���ƽ��״̬������A��B�������ɾ���ϵ����Ϊ5N/cm��B�����϶����컨��̶����ӣ���������ֱ����ļн�Ϊ60�㣬A������ֱ��gȡ10m/s2��������˵����ȷ���ǣ�������
��ͼ��ʾ��������Ϊ1kg��С��a��b���ᵯ��A��B������F�������´���ƽ��״̬������A��B�������ɾ���ϵ����Ϊ5N/cm��B�����϶����컨��̶����ӣ���������ֱ����ļн�Ϊ60�㣬A������ֱ��gȡ10m/s2��������˵����ȷ���ǣ�������| A�� | A�����쳤��Ϊ3cm | B�� | ����F=10$\sqrt{3}$N | ||
| C�� | B���ɵ��쳤��Ϊ4cm | D�� | ͻȻ��ȥ����F˲�䣬b����ٶ�Ϊ0 |
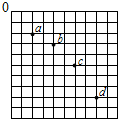 �ڡ�̽��ƽ���˶����˶����ɡ���ʵ���У���������С��ƽ���˶���һ���ֹ켣����֪ͼ��С����ı߳�L=10cm����С��ƽ�ij��ٶȴ�СΪv0=2m/s��ȡg=10m/s2����С����׳�������Ϊ��0.1m��0.1875m����
�ڡ�̽��ƽ���˶����˶����ɡ���ʵ���У���������С��ƽ���˶���һ���ֹ켣����֪ͼ��С����ı߳�L=10cm����С��ƽ�ij��ٶȴ�СΪv0=2m/s��ȡg=10m/s2����С����׳�������Ϊ��0.1m��0.1875m���� ��ͼ��ʾ��һ������n=30�ľ����߿���ܴ�ֱ�ڴų�����OO������ת������Ȧ���Ϊ0.02m2���Ÿ�Ӧǿ�ȵĴ�СB=2T�����ٶȦ�=100rad/s��������Ȧ���������濪ʼ��ʱ������
��ͼ��ʾ��һ������n=30�ľ����߿���ܴ�ֱ�ڴų�����OO������ת������Ȧ���Ϊ0.02m2���Ÿ�Ӧǿ�ȵĴ�СB=2T�����ٶȦ�=100rad/s��������Ȧ���������濪ʼ��ʱ������ �����ȫ��ͬ�ij�ľ�����ν����ŷ���ˮƽ�����ϣ�ÿ��ľ��ij���Ϊ0.525m������Ϊ0.6kg���ڵ�һ�鳤ľ�������˷���һ����Ϊ0.98kg��С��飮��֪С����볤ľ���Ķ�Ħ������Ϊ0.2����ľ��������Ķ�Ħ������Ϊ0.1�������Ħ�����뻬��Ħ������ȣ�һ������Ϊ0.02kg���ӵ���150m/s��ˮƽ�ٶȻ���С��鲢������С���һ���ڳ�ľ����滬�У��������ٶ�gȡ10m/s2��
�����ȫ��ͬ�ij�ľ�����ν����ŷ���ˮƽ�����ϣ�ÿ��ľ��ij���Ϊ0.525m������Ϊ0.6kg���ڵ�һ�鳤ľ�������˷���һ����Ϊ0.98kg��С��飮��֪С����볤ľ���Ķ�Ħ������Ϊ0.2����ľ��������Ķ�Ħ������Ϊ0.1�������Ħ�����뻬��Ħ������ȣ�һ������Ϊ0.02kg���ӵ���150m/s��ˮƽ�ٶȻ���С��鲢������С���һ���ڳ�ľ����滬�У��������ٶ�gȡ10m/s2��