题目内容
19. 如图所示,质量为M的劈块左右面的倾角分别为θ1=30°θ2=45°,质量分别为m1=$\sqrt{3}$kg和m2=2.0kg的两个物块,同时分别从左右的顶端从静止开始下滑,劈块始终与水平面保持相对静止,各接触面间的动摩擦因数均为μ=0.20,求两物块下滑过程中(m1和m2均未达到底端),劈块受到的地面摩擦力.(g=10m/s2)
如图所示,质量为M的劈块左右面的倾角分别为θ1=30°θ2=45°,质量分别为m1=$\sqrt{3}$kg和m2=2.0kg的两个物块,同时分别从左右的顶端从静止开始下滑,劈块始终与水平面保持相对静止,各接触面间的动摩擦因数均为μ=0.20,求两物块下滑过程中(m1和m2均未达到底端),劈块受到的地面摩擦力.(g=10m/s2)
分析 选M、m1和m2构成的整体为研究对象,根据各种性质的力产生的条件,在水平方向,整体除受到地面的静摩擦力外,不可能再受到其他力,如果受到静摩擦力,那么此力便是整体在水平方向受到的合外力,根据系统牛顿第二定律,取水平向左的方向为正方向列式即可求解.
解答 解:选M、m1和m2构成的整体为研究对象,把在相同时间内,M保持静止,m1和m2分别以不同的加速度下滑三个过程视为一个整体过程来研究.根据各种性质的力产生的条件,在水平方向,整体除受到地面的静摩擦力外,不可能再受到其他力;如果受到静摩擦力,那么此力便是整体在水平方向受到的合外力.
根据系统牛顿第二定律,取水平向左的方向为正方向,则有:
F合x=Ma′+m1a1x-m2a2x
其中a′、a1x和a2x分别为M、m1和m2在水平方向的加速度的大小,而
a′=0,a1x=g (sin30°-μcos30°) cos30°,a2x=g(sin45°-μcos45°) cos45°
所以:
F合=m1g(sin30°-μcos30°)cos30°-m2g (sin45°-μcos45°) cos45°
=$\sqrt{3}$×10×($\frac{1}{2}$-0.2×$\frac{\sqrt{3}}{2}$)×$\frac{\sqrt{3}}{2}$-2.0×10×($\frac{\sqrt{2}}{2}$-0.2×$\frac{\sqrt{2}}{2}$)×$\frac{\sqrt{2}}{2}$=-2.1N
负号表示整体在水平方向受到的合外力的方向与选定的正方向相反,
所以劈块受到地面的摩擦力的大小为2.1N,方向水平向右.
答:两物块下滑过程中,劈块受到的地面摩擦力大小为2.1N,方向水平向右.
点评 本题考查整体隔离法的应用,静止时现已整体为研究对象,所以整体没有运动趋势,不受摩擦力作用,两物块下滑过程中,分析两物块的受力情况,把加速度分解为水平和竖直方向,由牛顿第二定律列公式可求得水平方向的合力,由此可知要想静止不动,静摩擦力必须平衡该力.

 名校课堂系列答案
名校课堂系列答案| A. | 小球的线速度为1.5 m/s | |
| B. | 小球在3 s的时间内通过的路程为6 m | |
| C. | 小球做圆周运动的周期为5 s | |
| D. | 以上说法都不正确 |
 一带电粒子仅在电场力作用下以初速度v0从t=0时刻开始运动,其v-t图象如图所示.如粒子在t0时刻运动到A点,5t0时刻运动到B点.以下说法中正确的是( )
一带电粒子仅在电场力作用下以初速度v0从t=0时刻开始运动,其v-t图象如图所示.如粒子在t0时刻运动到A点,5t0时刻运动到B点.以下说法中正确的是( )| A. | A、B两点的电场强度大小关系为:EA=EB | |
| B. | A、B两点的电势关系为:φA>φB | |
| C. | t0到5t0时间内,电场力做的总功为正 | |
| D. | t0到5t0时间内,电势能先减小后增大 |
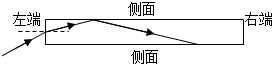 如图是一段长为L的直光导纤维内芯,一单色光从左端面射入光纤,已知光纤对单色光的折射率为n,光在真空中传播速度大小为c. 该单色光以任意不为零的入射角从左端射入,均能在侧面发生全反射,并从右端面射出.则( )
如图是一段长为L的直光导纤维内芯,一单色光从左端面射入光纤,已知光纤对单色光的折射率为n,光在真空中传播速度大小为c. 该单色光以任意不为零的入射角从左端射入,均能在侧面发生全反射,并从右端面射出.则( )| A. | 增加单色光的频率,光在光纤中的传播速度将增大 | |
| B. | 改变光在左端面的入射角,光在光纤中的传播时间不变 | |
| C. | 该单色光在光纤中传播的最短时间为$\frac{nL}{c}$ | |
| D. | n$<\sqrt{2}$ |
 如图所示,Ⅰ和Ⅱ是一对异名磁极,ab为放在其间的金属棒.ab和cd用导线连成一个闭合回路.当ab棒向左运动时,cd导线受到向下的磁场力.则有( )
如图所示,Ⅰ和Ⅱ是一对异名磁极,ab为放在其间的金属棒.ab和cd用导线连成一个闭合回路.当ab棒向左运动时,cd导线受到向下的磁场力.则有( )| A. | 由此可知d电势高于c电势 | |
| B. | 由此可知Ⅰ是S极 | |
| C. | 由此可知Ⅰ是N极 | |
| D. | 当cd棒向下运动时,ab导线受到向左的磁场力 |
| A. | 牛顿总结出了万有引力定律并测出了万有引力常量 | |
| B. | 历史上首先正确认识力和运动的关系,推翻“力是维持物体运动的原因”观点的物理学家是伽利略 | |
| C. | 安培最早发现了电流周围存在着磁场 | |
| D. | 法拉第发现了电磁感应现象,总结出了电磁感应定律 |
 如图所示,质量为m的小球在光滑水平面上向左运动,速度为v1,与竖直墙壁碰撞后以速度v2水平向右弹回,小球在与墙壁碰撞的过程中,动量改变量的大小为m(v1+v2),动量改变量的方向水平向右.
如图所示,质量为m的小球在光滑水平面上向左运动,速度为v1,与竖直墙壁碰撞后以速度v2水平向右弹回,小球在与墙壁碰撞的过程中,动量改变量的大小为m(v1+v2),动量改变量的方向水平向右. 如图所示的装置为一个光滑圆弧轨道与水平轨道相连,小物块A、B质量均为m,水平轨道上PQ段长为l与小物块间的动摩擦因数为μ,其余段光滑.初始时,轻质弹簧处于原长,其左端带有轻质挡板静止于Q点,轻质弹簧右端固定在O点;小物块A从光滑圆弧轨道上高为h处无初速度滑下,与静止在光滑圆弧轨道末端的B发生完全非弹性碰撞,之后A、B一起向右运动,不再返回P点左侧.
如图所示的装置为一个光滑圆弧轨道与水平轨道相连,小物块A、B质量均为m,水平轨道上PQ段长为l与小物块间的动摩擦因数为μ,其余段光滑.初始时,轻质弹簧处于原长,其左端带有轻质挡板静止于Q点,轻质弹簧右端固定在O点;小物块A从光滑圆弧轨道上高为h处无初速度滑下,与静止在光滑圆弧轨道末端的B发生完全非弹性碰撞,之后A、B一起向右运动,不再返回P点左侧. 如图所示,在直角坐标系XOY中,X轴上方有匀强磁场,磁感应强度的大小为B,磁场方向垂直于纸面向外.许多质量m、电荷量为+q的粒子,以相同的速率V沿纸面内,由X轴负方向与y轴正方向之间各个方向从原点O射入磁场区域.不计重力及粒子间的相互作用.下列图中阴影部分表示带电粒子在磁场中可能经过的区域,其中R=$\frac{mv}{qB}$,正确的图是( )
如图所示,在直角坐标系XOY中,X轴上方有匀强磁场,磁感应强度的大小为B,磁场方向垂直于纸面向外.许多质量m、电荷量为+q的粒子,以相同的速率V沿纸面内,由X轴负方向与y轴正方向之间各个方向从原点O射入磁场区域.不计重力及粒子间的相互作用.下列图中阴影部分表示带电粒子在磁场中可能经过的区域,其中R=$\frac{mv}{qB}$,正确的图是( )


