题目内容
19．甲、乙两颗人造地球卫星绕地球做匀速圆周运动，它们的质量之比m1：m2=2：3，运行轨道的半径之比r1：r2=4：9，则它们的向心力之比F1：F2=27：8，运动的周期之比T1：T2=8：27．分析 根据万有引力提供向心力得出线速度、角速度、周期与轨道半径的关系，从而得出线速度、角速度、周期之比．
解答 解：根据万有引力提供向心力得出，F=$\frac{GMm}{{R}^{2}}$，所以F1：F2=$\frac{2}{3}×\frac{{9}^{2}}{{4}^{2}}$=27：8，
根据万有引力提供向心力得出，T=$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$，所以周期之比为T1：T2=8：27
故答案为：27：8，8：27
点评 解决本题的关键掌握万有引力提供向心力这一理论，并能灵活运用．
练习册系列答案
相关题目
9．
如图所示，在两个固定的异种点电荷Q1、Q2的连线上有A、B两点．将一个带负电的试探电荷q由A静止释放，它从A点运动到B点的过程中，可能（ ）
如图所示，在两个固定的异种点电荷Q1、Q2的连线上有A、B两点．将一个带负电的试探电荷q由A静止释放，它从A点运动到B点的过程中，可能（ ）| A． | 先加速运动再减速运动 | B． | 加速度一直增大 | ||
| C． | 电势能先增大后减小 | D． | 在B点电势能比在A点的电势能大 |
如图所示，质量M=8kg的小车放在水平光滑的平面上，在小车左端加一水平推力F=8N，当小车向右运动的速度达到1.5m/s时，在小车前端轻轻地放上一个大小不计，质量为m=2kg的小物块，物块与小车间的动摩擦因数 μ=0.2，小车足够长（取g=10m/s2）．求：
．
11．依据热学知识可知，下列说法正确的是（ ）
| A． | 已知一定质量物质的体积和该物质分子的体积，一定能估算出阿伏伽德罗常数 | |
| B． | 当分子力表现为斥力时，分子间距减小，分子势能将增大 | |
| C． | 要使一定质量的气体分子平均动能增大，外界一定向气体传热 | |
| D． | 外界对气体做功，气体压强增大，内能也增加 |
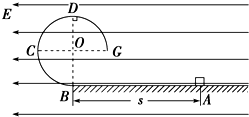如图所示，BCDG是光滑绝缘的$\frac{3}{4}$圆形轨道，位于竖直平面内，轨道半径为R，下端与水平绝缘轨道在B点平滑连接，整个轨道处在水平向左的匀强电场中．现有一质量为m、带正电的小滑块（可视为质点）置于水平轨道上，滑块受到的电场力大小为$\frac{3}{4}$mg，滑块与水平轨道间的动摩擦因数为0.5，重力加速度为g．