题目内容
14.在光滑水平面上,一质量为m、速度大小为v的A球与质量为2m静止的B球碰撞后粘在一起共速运动,则碰撞时A对B做的功为( )| A. | $\frac{{m{v^2}}}{18}$ | B. | $\frac{{m{v^2}}}{9}$ | C. | $\frac{{m{v^2}}}{6}$ | D. | $\frac{{m{v^2}}}{3}$ |
分析 A、B碰撞过程动量守恒,由动量守恒定律可以求出碰撞后的速度.根据动能定理求解碰撞时A对B做的功.
解答 解:A、B组成的系统碰撞过程动量守恒,以A的初速度方向为正方向,由动量守恒定律得:
mAv=(mA+mB)v′,
解得:v′=$\frac{1}{3}$v,
对B,根据动能定理得:
W=$\frac{1}{2}•2mv{′}^{2}=\frac{1}{2}×2m×\frac{{v}^{2}}{9}=\frac{m{v}^{2}}{9}$,故B正确.
故选:B
点评 本题考查了求速度和物体增加的动能,分析清楚物体运动过程、应用动量守恒定律与动能定理即可解题,注意要规定正方向,难度适中.

练习册系列答案
相关题目
4.为研究太阳系内行星的运动,需要知道太阳的质量.已知地球半径为R,地球质量为m,太阳与地球中心间距为r,地球表面的重力加速度为g,地球绕太阳公转的周期为T.则太阳的质量为( )
| A. | $\frac{{4{π^2}{r^3}}}{{{T^2}{R^2}g}}$ | B. | $\frac{{{T^2}{R^2}g}}{{4{π^2}m{r^3}}}$ | C. | $\frac{{4{π^2}m{r^3}}}{{{T^2}{R^2}g}}$ | D. | $\frac{{4{π^2}mg{R^2}}}{{{r^3}{T^2}}}$ |
2.关于热力学温标和摄氏温标,下列说法正确的是( )
| A. | 热力学温度与摄氏温度的关系是T=t-273.15K | |
| B. | 热力学温度升高1K大于摄氏温度升高1℃ | |
| C. | 热力学温度升高1K等于摄氏温度升高1℃ | |
| D. | 某物体摄氏温度为10℃,即热力学温度为10K |
9.如图所示为物体分子势能与分子间距离之间的关系,下列判断正确的是( )


| A. | 当r<r0时,r越小,则分子势能Ep越大 | |
| B. | 当r>r0时,r越小,则分子势能Ep越大 | |
| C. | 当r=r0时,分子势能Ep最小 | |
| D. | 当r→∞时,分子势能Ep最小 |
6.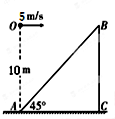 如图所示,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的o点,以5m/s的速度水平抛出一个小球,飞行一段时间后撞在斜面上,这段飞行所用的时间为(g=10m/s2)( )
如图所示,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的o点,以5m/s的速度水平抛出一个小球,飞行一段时间后撞在斜面上,这段飞行所用的时间为(g=10m/s2)( )
 如图所示,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的o点,以5m/s的速度水平抛出一个小球,飞行一段时间后撞在斜面上,这段飞行所用的时间为(g=10m/s2)( )
如图所示,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的o点,以5m/s的速度水平抛出一个小球,飞行一段时间后撞在斜面上,这段飞行所用的时间为(g=10m/s2)( )| A. | 2s | B. | $\sqrt{2}$s | C. | 1s | D. | 0.5s |
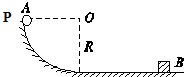 如图,t=0s时小球A从半径为R=0.8m的$\frac{1}{4}$光滑圆弧轨道的上端P点以v0=3m/s的初速度开始滑下,到达光滑水平面上以后,与静止于该水平面上的钢块B发生碰撞,碰撞后小球A被反向弹回,B的质量mB=18kg.A沿原路进入轨道运动恰能上升到它下滑时的出发点(此时速度为零).设A、B碰撞机械能不损失,g取10m/s2,求:
如图,t=0s时小球A从半径为R=0.8m的$\frac{1}{4}$光滑圆弧轨道的上端P点以v0=3m/s的初速度开始滑下,到达光滑水平面上以后,与静止于该水平面上的钢块B发生碰撞,碰撞后小球A被反向弹回,B的质量mB=18kg.A沿原路进入轨道运动恰能上升到它下滑时的出发点(此时速度为零).设A、B碰撞机械能不损失,g取10m/s2,求: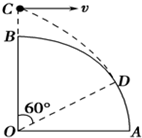 如图所示为四分之一圆柱体OAB的竖直截面,半径为R,在B点上方的C点水平抛出一个小球,小球轨迹恰好在D点与圆柱体相切,OD与OB的夹角为60°.求C点到B点的距离是多少?
如图所示为四分之一圆柱体OAB的竖直截面,半径为R,在B点上方的C点水平抛出一个小球,小球轨迹恰好在D点与圆柱体相切,OD与OB的夹角为60°.求C点到B点的距离是多少?