��Ŀ����
11�� ��ͼ��ʾ��ijͬѧ���о�ƽ���˶���ʵ���У���С����ֽ�ϻ���С����ƽ���˶��Ĺ켣�Ժ����ڹ켣��ȡ��a��b��c��d�ĸ��㣨�켣�Ѳ�ȥ������֪С����ֽ�ı߳�L���������ٶ�Ϊg���������С����ֽ�ϵ���Ϣ��ͨ����������������漸�����⣺
��ͼ��ʾ��ijͬѧ���о�ƽ���˶���ʵ���У���С����ֽ�ϻ���С����ƽ���˶��Ĺ켣�Ժ����ڹ켣��ȡ��a��b��c��d�ĸ��㣨�켣�Ѳ�ȥ������֪С����ֽ�ı߳�L���������ٶ�Ϊg���������С����ֽ�ϵ���Ϣ��ͨ����������������漸�����⣺��1��С���a��b��b��c��c��d��������ʱ����ȣ����ȡ�����ȡ�����
��2��С��ƽ���˶��ij��ٶ�v0=2$\sqrt{gL}$��
��3�����׳��㵽b����������ʱ��t=$\frac{3}{2}\sqrt{\frac{L}{g}}$��
���� ƽ���˶���ˮƽ������������ֱ���˶�������ֱ�����������������˶������ˮƽλ�ƵĴ�С�ȽϾ�����ʱ�䣻
������ֱ�������������ʱ���ڵ�λ��֮����һ���������ȵ�ʱ������
����ˮƽλ�ƺ�ʱ�����ƽ���˶��ij��ٶȣ�
AC������ֱ�����ϵ�ƽ���ٶȵ���B����ֱ�����ϵ�˲ʱ�ٶȣ��������ٶȹ�ʽ���������ʱ�䣮
��� �⣺��1��С���a��b��b��c��c��dˮƽλ����ȣ���Ϊˮƽ������������ֱ���˶������Ծ�����ʱ����ȣ�
��2�����ݡ�y=L=gT2�ã�T=$\sqrt{\frac{L}{g}}$��
ƽ���˶��ij��ٶ�Ϊ��v0=$\frac{2L}{T}$=2$\sqrt{gL}$��
��3��b������ֱ�����ϵķ��ٶ�Ϊ��vby=$\frac{{y}_{ac}}{2T}$=$\frac{3L}{2T}$=$\frac{3}{2}\sqrt{gL}$��
����ˮƽ��������ֱ���˶�����˴��׳��㵽b����������ʱ���ǣ�t=$\frac{{v}_{by}}{g}$=$\frac{3}{2}\sqrt{\frac{L}{g}}$
�ʴ�Ϊ����1����ȣ���2��2$\sqrt{gL}$����3��$\frac{3}{2}\sqrt{\frac{L}{g}}$��
���� �������Ĺؼ�֪��ƽ���˶���ˮƽ�������ֱ�����ϵ��˶����ɣ�����˶�ѧ��ʽ�����������⣮

 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д�| A�� | tA=tB=tC | B�� | tA=tC��tB | C�� | tA=tB��tC | D�� | tA��tB��tC |
 ��ͼ��ʾ���⻬��ˮƽ���ϣ�С��m������F������������Բ���˶�����С��P��ʱFͻȻ�����仯�����й���С���˶������˵����ȷ���ǣ�������
��ͼ��ʾ���⻬��ˮƽ���ϣ�С��m������F������������Բ���˶�����С��P��ʱFͻȻ�����仯�����й���С���˶������˵����ȷ���ǣ�������| A�� | ������ͻȻ��ʧ��С���ع켣Pa������ֱ���˶� | |
| B�� | ������ͻȻ��С��С���ع켣Pa�������˶� | |
| C�� | ������ͻȻ��ʧ��С���ع켣Pb�������˶� | |
| D�� | ������ͻȻ���С�����ع켣Pc�������˶� |
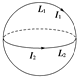 һ�����������˶�����ȦL1��һ���̶�����ȦL2�����Ե��ֱ���ã���������Ȧ��Բ���غϣ���ͼ��ʾ��������Ȧ��ͨ��ͼʾ����ĵ���ʱ���������ҿ�����ȦL1����������
һ�����������˶�����ȦL1��һ���̶�����ȦL2�����Ե��ֱ���ã���������Ȧ��Բ���غϣ���ͼ��ʾ��������Ȧ��ͨ��ͼʾ����ĵ���ʱ���������ҿ�����ȦL1����������| A�� | ���� | B�� | ˳ʱ��ת�� | C�� | ��ʱ��ת�� | D�� | ��ֽ����ƽ�� |
 ��ͼ��ʾ���⻬ˮƽ��OB���㹻���ֲ�б��BC����B�㣮�ᵯ����˹̶�����ֱǽ�棬�ֽ�����Ϊm1�Ļ���ѹ��������D�㣬Ȼ���ɾ�ֹ�ͷţ��������뵯�ɺ�B�㻬��б�棬���������߶ȣ�����ֹ��б���ϣ����ƻ�����B��Ļ�е����ʧ�����ò�����ͬ������Ϊm2�Ļ��飨m2��m1��ѹ��������ͬһ��D���ظ��������̣�����˵����ȷ���ǣ�������
��ͼ��ʾ���⻬ˮƽ��OB���㹻���ֲ�б��BC����B�㣮�ᵯ����˹̶�����ֱǽ�棬�ֽ�����Ϊm1�Ļ���ѹ��������D�㣬Ȼ���ɾ�ֹ�ͷţ��������뵯�ɺ�B�㻬��б�棬���������߶ȣ�����ֹ��б���ϣ����ƻ�����B��Ļ�е����ʧ�����ò�����ͬ������Ϊm2�Ļ��飨m2��m1��ѹ��������ͬһ��D���ظ��������̣�����˵����ȷ���ǣ�������| A�� | .����鵽��B��ʱ�ٶ���ͬ | |
| B�� | .��������б�����������߶���ͬ | |
| C�� | ��������������ߵ�Ĺ����п˷�������������ͬ | |
| D�� | ��������������ߵ�Ĺ����л�е����ʧ��ͬ |
 С��P��Q�ò����쳤�������������컨���ϣ�P�����������Q�������������P�����������Q������̣����������Ϊ�ʵ㣮��������ʹ���Ӿ���ˮƽ��ֱ����ͼ��ʾ���������ɾ�ֹ�ͷţ��ڸ��Թ켣����͵㣨������
С��P��Q�ò����쳤�������������컨���ϣ�P�����������Q�������������P�����������Q������̣����������Ϊ�ʵ㣮��������ʹ���Ӿ���ˮƽ��ֱ����ͼ��ʾ���������ɾ�ֹ�ͷţ��ڸ��Թ켣����͵㣨������| A�� | P����ٶ�һ��С��Q����ٶ� | |
| B�� | P��Ķ���һ��С��Q��Ķ��� | |
| C�� | P��������������һ������Q�������������� | |
| D�� | P������ļ��ٶ�һ��С��Q������ļ��ٶ� |
| A�� | С��Ľ��ٶ�Ϊ��=$\sqrt{\frac{R}{a}}$ | B�� | С����˶�����ΪT=2��$\sqrt{\frac{R}{a}}$ | ||
| C�� | С����ʱ��t��ͨ����·��Ϊs=t$\sqrt{\frac{R}{a}}$ | D�� | С����ʱ��t��ͨ����·��Ϊs=$\sqrt{Ra}$ |
 ��ͼ1��ʾ��С����Ϊ�ʵ㣩�ڹ⻬Բ�����ϵ�A��A��֮�������˶���С����˶���Ϊ��г�˶���ʹ����������������С�ó�������Ƶ�������֮��Ĺ�ϵ��ͼ2��ʾ����������Ƶ��Ϊf0ʱС��������ȥ��������С��������A��A���Ϊ���Ҷ˵㣬DΪ��͵㣬A��A�����Բ��O����������ֱ����֮��ļн�����Ҿ�Ϊ�ȣ����ȣ�5�㣩����֪�������ٶ�g����
��ͼ1��ʾ��С����Ϊ�ʵ㣩�ڹ⻬Բ�����ϵ�A��A��֮�������˶���С����˶���Ϊ��г�˶���ʹ����������������С�ó�������Ƶ�������֮��Ĺ�ϵ��ͼ2��ʾ����������Ƶ��Ϊf0ʱС��������ȥ��������С��������A��A���Ϊ���Ҷ˵㣬DΪ��͵㣬A��A�����Բ��O����������ֱ����֮��ļн�����Ҿ�Ϊ�ȣ����ȣ�5�㣩����֪�������ٶ�g����