题目内容
4.如图,在水平轨道右侧固定半径为R的竖直圆槽形光滑轨道,水平轨道的PQ段铺设特殊材料,调节其初始长度为l;水平轨道左侧有一轻质弹簧左端固定,弹簧处于自然伸长状态.可视为质点的小物块从轨道右侧A点以初速度v0冲上轨道,通过圆形轨道、水平轨道后压缩弹簧,并被弹簧以原速率弹回.已知R=0.4m,l=2.5m,v0=6m/s,物块质量m=1kg,与PQ段间的动摩擦因数μ=0.4,轨道其他部分摩擦不计.取g=10m/s2.求:
(1)物块经过圆轨道最高点B时对轨道的压力;
(2)物块从Q运动到P的时间及弹簧获得的最大弹性势能;
(3)调节仍以v0从右侧冲上轨道,调节PQ段的长度l,当l长度是多少时,物块恰能不脱离轨道返回A点继续向右运动.
分析 (1)对从初始位置到圆弧轨道的最高点过程,根据动能定理列式求解最高点的速度;在圆弧轨道的最高点,重力和弹力的合力提供向心力,根据牛顿第二定律列式求解弹力;
(2)只有在PQ阶段有机械能损失,对从Q到P过程,根据牛顿第二定律求解加速度,根据位移公式求解时间,根据速度公式求解末速度;从P点到最左端过程,弹簧获得的最大弹性势能等于在P位置的动能;
(3)先根据牛顿第二定律求解物体恰能经过圆弧最高点的速度,然后对运动的全程根据动能定理列式求解l的距离.
解答 解:(1)对从初始位置到圆弧轨道的最高点过程,根据动能定理,有:
-mg(2R)=$\frac{1}{2}m{v}_{1}^{2}-\frac{1}{2}m{v}_{0}^{2}$
在圆弧轨道的最高点,根据牛顿第二定律,有:
mg+N=m$\frac{{v}^{2}}{R}$
联立解得:
${v}_{1}=2\sqrt{5}m/s$
N=40N
根据牛顿第三定律,物块经过圆轨道最高点B时对轨道的压力为40N;
(2)从Q到P过程,滑块的加速度为:a=-μg=-4m/s2;
根据位移公式,有:x=${v}_{0}t+\frac{1}{2}a{t}^{2}$,代入数据解得:
t=0.5s或t=2.5s(不可能速度减小为零后反向加速,故舍去)
在P点的速度为:v2=v0+at=6-4×0.5=4m/s
故最大弹性势能为:${E}_{pm}=\frac{1}{2}m{v}_{2}^{2}=\frac{1}{2}×1×{4}^{2}=8J$
(3)物块恰能不脱离轨道返回A点,在圆轨道最高点的速度为:
${v}_{3}=\sqrt{gR}=\sqrt{10×0.4}=2m/s$
对从开始到第二次到圆轨道的最高点过程,根据动能定理,有:
-mg(2R)-μmg•2l=$\frac{1}{2}m{v}_{3}^{2}-\frac{1}{2}m{v}_{0}^{2}$
解得:
2l=$\frac{{v}_{0}^{2}-{v}_{3}^{2}}{2μg}$-$\frac{2R}{μ}$=$\frac{{6}^{2}-{2}^{2}}{2×0.4×10}-\frac{2×0.4}{0.4×10}$×10=2m
故l=1m
答:(1)物块经过圆轨道最高点B时对轨道的压力为40N;
(2)物块从Q运动到P的时间为1s,弹簧获得的最大弹性势能为8J;
(3)调节仍以v0从右侧冲上轨道,调节PQ段的长度l,当l长度是1m时,物块恰能不脱离轨道返回A点继续向右运动.
点评 本题综合考查了运动学公式、向心力公式、动能定理、牛顿第二定律,以及知道小球不脱离圆轨道的条件,综合性较强,对学生的能力要求较高,需加强训练.

| A. | 该行星的自转周期 | B. | 该行星的密度 | ||
| C. | 该星球的第一宇宙速度 | D. | 绕该行星运行的卫星的最小周期 |
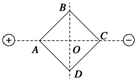 如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )
如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )| A. | A点的电场强度等于B点的电场强度 | |
| B. | B、D两点的电场强度及电势均相同 | |
| C. | 一电子由B点沿B→C→D路径移至D点,电势能先减小后增大 | |
| D. | 一电子由C点沿C→O→A路径移至A点,电场力对其先做负功后做正功 |
 如图所示,桌面离地高度为h,质量为m的小球,从离桌面H高处由静止下落.若以桌面为参考平面,那么小球落地时的重力势能及整个下落过程中重力势能的变化分别为( )
如图所示,桌面离地高度为h,质量为m的小球,从离桌面H高处由静止下落.若以桌面为参考平面,那么小球落地时的重力势能及整个下落过程中重力势能的变化分别为( )| A. | mgh,减少mg(H-h) | B. | mgh,增加mg(H+h) | C. | -mgh,增加mg(H-h) | D. | -mgh,减少mg(H+h) |
 如图所示,A,B,C,D是真空中一正四面体的四个顶点,现在在A,B两点分别固定电荷量为+q,-q的两个点电荷,则关于C,D两点的磁场和电势,下列说法正确的是( )
如图所示,A,B,C,D是真空中一正四面体的四个顶点,现在在A,B两点分别固定电荷量为+q,-q的两个点电荷,则关于C,D两点的磁场和电势,下列说法正确的是( )| A. | C,D两点的电场强度不同,电势相同 | |
| B. | C,D两点的电场强度相同,电势不同 | |
| C. | 将一正电荷从C点移到D点,电场力对该正电荷先做正功,然后做负功 | |
| D. | 将一正电荷从C点移到D点,电场力对该正电荷先做负功,然后做正功 |
 如图,固定有滑圆弧轨道的小车A静止在光的水平面上,轨道足够长,其下部分水平,有一小滑块B以某水平初速度滑上小车,滑轮不从圆弧上端滑出,则滑块B在车上运动的过程中( )
如图,固定有滑圆弧轨道的小车A静止在光的水平面上,轨道足够长,其下部分水平,有一小滑块B以某水平初速度滑上小车,滑轮不从圆弧上端滑出,则滑块B在车上运动的过程中( )| A. | 当滑块上升到最大高度时,滑块的速度为零 | |
| B. | 滑块运动过程中机械能守恒 | |
| C. | 滑块离开小车时的速度与滑上小车时的速度大小相等 | |
| D. | 滑块B在小车上运动的过程中,滑块与小车组成的系统动量不守恒 |
 如图所示,在内壁光滑的平底玻璃管内,装有一质量为10g的小球(可视为质点),将玻璃管开口端封闭后安装在转轴O上,转轴到管底的距离为25cm,让玻璃管在竖直面内匀速转动,求:
如图所示,在内壁光滑的平底玻璃管内,装有一质量为10g的小球(可视为质点),将玻璃管开口端封闭后安装在转轴O上,转轴到管底的距离为25cm,让玻璃管在竖直面内匀速转动,求:
