题目内容
8. 如图所示,长为L的轻杆,一端固定着一个小球,另一端可绕光滑的水平轴转动,使小球在竖直平面内运动.设小球在最高点的速度为v,则( )
如图所示,长为L的轻杆,一端固定着一个小球,另一端可绕光滑的水平轴转动,使小球在竖直平面内运动.设小球在最高点的速度为v,则( )| A. | v的最小值为0 | |
| B. | v若增大,此时所需的向心力将减小 | |
| C. | 当v由$\sqrt{gL}$逐渐增大时,杆对球的弹力也逐渐增大 | |
| D. | 当v由$\sqrt{gL}$逐渐减小时,杆对球的弹力也逐渐减小 |
分析 小球在竖直平面内作圆周运动,在最高点时,由于杆能支撑小球,小球速度的极小值为零;根据向心力公式Fn=m$\frac{{v}^{2}}{r}$分析速度增大时,向心力如何变化;
当v=$\sqrt{gL}$时,杆对球没有作用力,v由$\sqrt{gL}$逐渐增大时,杆对球有向下的拉力;v由$\sqrt{gL}$逐渐减小时,杆对球有向上的支持力,根据牛顿第二定律分析杆对球的弹力的变化情况.
解答 解:A、由于杆能支撑小球,因此v的极小值为零.故A正确.
B、根据向心力公式Fn=m$\frac{{v}^{2}}{L}$知,速度逐渐增大,向心力也逐渐增大.故B错误.
C、当v=$\sqrt{gL}$时,杆对球没有作用力,v由$\sqrt{gL}$逐渐增大,杆对球有向下的拉力,根据牛顿第二定律得:F+mg=m$\frac{{v}^{2}}{L}$,得F=m$\frac{{v}^{2}}{L}$-mg,可见,v增大,F增大.故C正确.
D、v由$\sqrt{gL}$逐渐减小时,杆对球有向上的支持力,有mg-F=m$\frac{{v}^{2}}{L}$,解得F=mg-m$\frac{{v}^{2}}{L}$,速度减小,则杆子的弹力增大.故D错误.
故选:AC.
点评 此题是轻杆模型,要掌握两个临界速度:一、小球恰好到达最高点的临界速度是零;二、杆对球没有弹力的临界速度v=$\sqrt{gL}$.根据牛顿第二定律分析弹力随速度的变化情况.

练习册系列答案
相关题目
7.下列说法正确的是( )
| A. | X射线是处于激发态的原子核辐射出来的 | |
| B. | 康普顿效应和电子的衍射现象说明光和电子都具有波动性 | |
| C. | 普朗克为了解释黑体辐射现象,第一次提出了能量量子化理论 | |
| D. | 汤姆孙根据阴极射线在电场和磁场中的偏转情况断定其本质是带负电的粒子流并测定了这种粒子的电荷量 |
16.同步卫星离地心距离为r,运行速率为v1,向心加速度为a1,轨道所在处的重力加速度为g1.地球的半径为R,第一宇宙速度为v2,地球赤道上的物体随地球自转的向心加速度为a2,地球表面的重力加速度为g2.则下列结果不正确的是( )
| A. | a1=g1 | B. | $\frac{{g}_{1}}{{g}_{2}}$=$\frac{{R}^{2}}{{r}^{2}}$ | C. | $\frac{{v}_{1}}{{v}_{2}}$=$\frac{r}{R}$ | D. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{r}{R}$ |
3.$\underset{210}{84}$Po核的半衰期为138天,经过α衰变生成未定的铅核($\underset{206}{82}$Pb),经过414天,100g$\underset{210}{84}$Po核未衰变的质量为( )
| A. | 12.5g | B. | 50g | C. | 75g | D. | 100g |
13.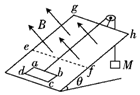 如图所示,光滑斜面的倾角为θ,在斜面上放置一矩形线框abcd,ab边的边长为l1,bc边的长为l2,线框的质量为m、电阻为R,线框通过细线与重物相连,重物的质量为M,斜面上ef线(ef平行底边)的右方有垂直斜面向上的匀强磁场宽度l3 (l3大于l2),磁感应强度为B.如果线框从静止开始运动,直至全部进入磁场,且进入磁场的最初一段时间是做匀速运动,则下列说法正确的是( )
如图所示,光滑斜面的倾角为θ,在斜面上放置一矩形线框abcd,ab边的边长为l1,bc边的长为l2,线框的质量为m、电阻为R,线框通过细线与重物相连,重物的质量为M,斜面上ef线(ef平行底边)的右方有垂直斜面向上的匀强磁场宽度l3 (l3大于l2),磁感应强度为B.如果线框从静止开始运动,直至全部进入磁场,且进入磁场的最初一段时间是做匀速运动,则下列说法正确的是( )
 如图所示,光滑斜面的倾角为θ,在斜面上放置一矩形线框abcd,ab边的边长为l1,bc边的长为l2,线框的质量为m、电阻为R,线框通过细线与重物相连,重物的质量为M,斜面上ef线(ef平行底边)的右方有垂直斜面向上的匀强磁场宽度l3 (l3大于l2),磁感应强度为B.如果线框从静止开始运动,直至全部进入磁场,且进入磁场的最初一段时间是做匀速运动,则下列说法正确的是( )
如图所示,光滑斜面的倾角为θ,在斜面上放置一矩形线框abcd,ab边的边长为l1,bc边的长为l2,线框的质量为m、电阻为R,线框通过细线与重物相连,重物的质量为M,斜面上ef线(ef平行底边)的右方有垂直斜面向上的匀强磁场宽度l3 (l3大于l2),磁感应强度为B.如果线框从静止开始运动,直至全部进入磁场,且进入磁场的最初一段时间是做匀速运动,则下列说法正确的是( )| A. | 线框abcd进入磁场前运动的加速度为 $\frac{Mg-mgsinθ}{m}$ | |
| B. | 线框在进入磁场过程中的运动速度v=$\frac{(Mg-mgsinθ)R}{{B}^{2}{{l}_{1}}^{2}}$ | |
| C. | 线框做匀速运动的时间为$\frac{{B}^{2}{{l}_{1}}^{2}{l}^{2}}{(Mg-mgsinθ)R}$ | |
| D. | 该过程产生的焦耳热Q=(Mg-mgsin θ)l3 |
17. 如图所示,物体A和B的质量均为m,且分别用轻绳连接跨过定滑轮(不计绳子与滑轮、滑轮与轴之间的摩擦),当用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中( )
如图所示,物体A和B的质量均为m,且分别用轻绳连接跨过定滑轮(不计绳子与滑轮、滑轮与轴之间的摩擦),当用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中( )
 如图所示,物体A和B的质量均为m,且分别用轻绳连接跨过定滑轮(不计绳子与滑轮、滑轮与轴之间的摩擦),当用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中( )
如图所示,物体A和B的质量均为m,且分别用轻绳连接跨过定滑轮(不计绳子与滑轮、滑轮与轴之间的摩擦),当用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中( )| A. | 物体A也做匀速直线运动 | |
| B. | 绳子拉力始终大于物体A所受的重力 | |
| C. | 绳子对A的拉力逐渐减小 | |
| D. | 地面对物体B的支持力逐渐增大 |
18.关于电动势,下列说法错误的是( )
| A. | 电源电动势的数值等于内、外电压之和 | |
| B. | 电源电动势与外电路的组成有关 | |
| C. | 外电路开路时,电源两极间的电压等于电源电动势 | |
| D. | 电动势在数值上等于非静电力把1C的正电荷在电源内从负极移送到正极所做的功 |





 在研究平抛物体运动的实验中,用闪光相机记录小球的运动轨迹,小方格的边长L=10厘米,若小球在平抛运动途中的各个位置如图中的a、b、c、d所示,则小球平抛的初速度为v0=2m/s,相机的闪光周期为0.1s,小球在b点竖直方向的速度V=1.5m/s.
在研究平抛物体运动的实验中,用闪光相机记录小球的运动轨迹,小方格的边长L=10厘米,若小球在平抛运动途中的各个位置如图中的a、b、c、d所示,则小球平抛的初速度为v0=2m/s,相机的闪光周期为0.1s,小球在b点竖直方向的速度V=1.5m/s.