题目内容
19.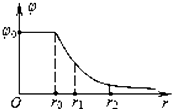 若取无穷远处为零电势,某一直线上各点的电势φ分布规律可用图中曲线表示,r表示该直线上某点到原点O的距离,r1、r2分别是该直线上A、B两点离原点O的距离.下列说法中正确的是( )
若取无穷远处为零电势,某一直线上各点的电势φ分布规律可用图中曲线表示,r表示该直线上某点到原点O的距离,r1、r2分别是该直线上A、B两点离原点O的距离.下列说法中正确的是( )| A. | O-r0这个区域的电场强度最大 | |
| B. | A点的电场强度可能等于B点的电场强度 | |
| C. | 若r2-r1=r1-r0,则φA-φB=φ0-φA | |
| D. | 将α粒子从A点移到B点,电场力做正功 |
分析 φ-r图象斜率大小等于场强.沿电场线方向电势逐渐降低.由U=Ed分析电势差的关系.根据电场力方向和运动方向关系判断电场力做功情况.
解答 解:A、根据场强公式E=$\frac{U}{d}$知,图象斜率大小等于场强,则得O-r0这个区域的电场强度为零,故A错误.
B、由于图象斜率大小等于场强,则A点的电场强度大于B点的电场强度,故B错误.
C、由于图象斜率大小等于场强,从O到A再到B,电场强度逐渐减小;故若r2-r1=r1-r0,则由U=Ed知,φA-φB<φ0-φA,故C错误;
D、α粒子从A移到B的过程中,电势降低,其电势能减小,所以电场力做正功,故D正确.
故选:D.
点评 本题关键是明确φ-x图象的斜率表示电场强度,然后结合电势与电场线关系分析.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.健身球是现在非常流行的健身保健器具之一,它有很好的弹性,已知某健身球的重力为G0.使用健身球的人重力为G,当人从球的正上方由静止开始压上健身球后(全身离地),下列说法正确的是( )
| A. | 地面对健身球的支持力总是等于G0+G | |
| B. | 健身球对该人的支持力总是等于G | |
| C. | 健身球被压到最扁过程中地面对球的支持力逐渐增大 | |
| D. | 该人在健身球上下降的原因是压健身球的力大于健身球对人的支持力 |
14. 如图是氢原子的能级图.设从n=4到n=1跃迁辐射电磁波波长为λ1,从n=4到n=2跃迁辐射电磁波波长为λ2,从n=2到n=1跃迁辐射电磁波波长为λ3.下列关系式中正确的是( )
如图是氢原子的能级图.设从n=4到n=1跃迁辐射电磁波波长为λ1,从n=4到n=2跃迁辐射电磁波波长为λ2,从n=2到n=1跃迁辐射电磁波波长为λ3.下列关系式中正确的是( )
 如图是氢原子的能级图.设从n=4到n=1跃迁辐射电磁波波长为λ1,从n=4到n=2跃迁辐射电磁波波长为λ2,从n=2到n=1跃迁辐射电磁波波长为λ3.下列关系式中正确的是( )
如图是氢原子的能级图.设从n=4到n=1跃迁辐射电磁波波长为λ1,从n=4到n=2跃迁辐射电磁波波长为λ2,从n=2到n=1跃迁辐射电磁波波长为λ3.下列关系式中正确的是( )| A. | λ1<λ3 | B. | λ2>λ3 | C. | λ1=λ2+λ3 | D. | $\frac{1}{λ_3}=\frac{1}{λ_1}+\frac{1}{λ_2}$ | ||||
| E. | $\frac{1}{λ_3}=\frac{1}{λ_1}-\frac{1}{λ_2}$ |
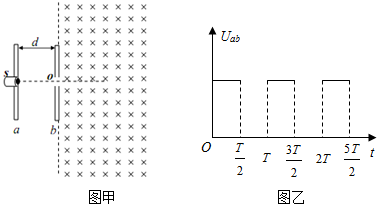
 如图1所示,一个圆形线圈的匝数n=1000,线圈面积S=0.02m2,线圈的电阻r=1Ω,线圈外接一个阻值R=4Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间变化规律如图2所示;求:
如图1所示,一个圆形线圈的匝数n=1000,线圈面积S=0.02m2,线圈的电阻r=1Ω,线圈外接一个阻值R=4Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间变化规律如图2所示;求: 在如图所示的电路中,电源的电动势E=28V,内阻r=2Ω,电阻R1=12Ω,R2=R4=4Ω,R3=8Ω,C为平行板电容器,其电容C=3.0pF,虚线到两极板的距离相等,极板长L=0.20m,两极板的间距d=1.0×l0-2m,g取10m/s2.
在如图所示的电路中,电源的电动势E=28V,内阻r=2Ω,电阻R1=12Ω,R2=R4=4Ω,R3=8Ω,C为平行板电容器,其电容C=3.0pF,虚线到两极板的距离相等,极板长L=0.20m,两极板的间距d=1.0×l0-2m,g取10m/s2. 如图所示为儿童娱乐的滑梯示意图,其中AB为光滑斜面滑槽,与水平方向夹角为37°,斜面AB与水平滑槽BC有一小圆弧连接,粗糙水平滑槽BC与半径为0.2m的$\frac{1}{4}$圆弧CD相切,ED为地面.已知儿童在水平滑槽上滑动时的动摩擦因数为0.5,AB两点的竖直高度h=0.6m,不计空气阻力,求:
如图所示为儿童娱乐的滑梯示意图,其中AB为光滑斜面滑槽,与水平方向夹角为37°,斜面AB与水平滑槽BC有一小圆弧连接,粗糙水平滑槽BC与半径为0.2m的$\frac{1}{4}$圆弧CD相切,ED为地面.已知儿童在水平滑槽上滑动时的动摩擦因数为0.5,AB两点的竖直高度h=0.6m,不计空气阻力,求: 如图所示,等离子气流(由高温高压的等电量的正、负离子组成)由左方连续不断的以速度v0射入P1和P2两极板间的匀强磁场中,ab和cd的作用情况为:0~1s内互相排斥,1~3s内互相吸引,3~4s内互相排斥.规定向左为磁感应强度B的正方向,线圈A内磁感应强度B随时间t变化的图象可能是( )
如图所示,等离子气流(由高温高压的等电量的正、负离子组成)由左方连续不断的以速度v0射入P1和P2两极板间的匀强磁场中,ab和cd的作用情况为:0~1s内互相排斥,1~3s内互相吸引,3~4s内互相排斥.规定向左为磁感应强度B的正方向,线圈A内磁感应强度B随时间t变化的图象可能是( )