题目内容
(1)一物体与轻质弹簧相连静放在足够长的光滑斜面上,若外力将物体拉离平衡位置,撤去外力后物体开始运动,不计空气阻力,论证物体的运动是否是简谐运动(写出论证过程才能得分)
(2)一列横波上有相距4m的A、B两点,波的传播方向是由A向B,波长大于2m,如图所示的是A、B两质点的振动图象,求:这列波的波v.

(2)一列横波上有相距4m的A、B两点,波的传播方向是由A向B,波长大于2m,如图所示的是A、B两质点的振动图象,求:这列波的波v.
分析:(1)振子振动时,弹簧的弹力提供回复力,根据胡克定律和牛顿第二定律得到振子的回复力与位移的关系,即可证明物体的运动是简谐运动.
(2)由振动图象读出周期.根据A、B两质点状态关系,得到波长的通项,结合条件波长大于2m,求出波长的特殊值,求出波速.
(2)由振动图象读出周期.根据A、B两质点状态关系,得到波长的通项,结合条件波长大于2m,求出波长的特殊值,求出波速.
解答:解:(1)设物体的质量为m,弹簧的劲度系数为k,振子振动时,弹簧的弹力提供回复力,振子的位移大小等于弹簧的形变量,而回复力与位移方向相反,设振子的位移为x,则有
F=-kx
所以物体的运动是简谐运动.
(2)由振动图象得:质点的振动周期T=0.4s.由振动图象可知,B点比A点晚振动的时间△t=(k+
)T,(k=1,2,3,…)
所以A、B间的距离为△x=(k+
)λ(k=0、1、2、3、…)
则波长为λ=
=
m
因为λ>2m,所以k=0,1
当k=0时,λ1=
m,v1=
=
m/s;当k=1时,λ2=
m,v2=
m/s.
T答:(1)物体的运动是简谐运动,证明见上.
(2)这列波的波v为
m/s或
m/s.
F=-kx
所以物体的运动是简谐运动.
(2)由振动图象得:质点的振动周期T=0.4s.由振动图象可知,B点比A点晚振动的时间△t=(k+
| 3 |
| 4 |
所以A、B间的距离为△x=(k+
| 3 |
| 4 |
则波长为λ=
| 4△x |
| 4k+3 |
| 16 |
| 4n+3 |
因为λ>2m,所以k=0,1
当k=0时,λ1=
| 16 |
| 3 |
| λ1 |
| T |
| 40 |
| 3 |
| 16 |
| 3 |
| 40 |
| 7 |
T答:(1)物体的运动是简谐运动,证明见上.
(2)这列波的波v为
| 40 |
| 3 |
| 40 |
| 7 |
点评:第1题根据简谐运动的特征:F=-kx判断物体的运动是简谐运动.第2题关键要能根据两质点的振动状态,确定出波长的通项,可以通过画波形的方法分析.

练习册系列答案
相关题目
 如图所示,光滑水平面MN上放两相同小物块A、B,左端挡板处有一弹射装置P,右端N处与水平传送带理想连接,传送带水平部分长度L=8m,沿逆时针方向以恒定速度v=6m/s匀速转动.物块A、B(大小不计)与传送带间的动摩擦因数μ=0.2.物块A、B质量mA=mB=1kg.开始时A、B静止,A、B间有一压缩轻质弹簧处于锁定状态,贮有弹性势能Ep=16J.现解除弹簧锁定,弹开A、B,同时迅速撤走弹簧.求:
如图所示,光滑水平面MN上放两相同小物块A、B,左端挡板处有一弹射装置P,右端N处与水平传送带理想连接,传送带水平部分长度L=8m,沿逆时针方向以恒定速度v=6m/s匀速转动.物块A、B(大小不计)与传送带间的动摩擦因数μ=0.2.物块A、B质量mA=mB=1kg.开始时A、B静止,A、B间有一压缩轻质弹簧处于锁定状态,贮有弹性势能Ep=16J.现解除弹簧锁定,弹开A、B,同时迅速撤走弹簧.求: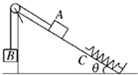 如图所示,固定斜面的倾角θ=30°,物体A与斜面之间的动摩擦因数为μ=
如图所示,固定斜面的倾角θ=30°,物体A与斜面之间的动摩擦因数为μ= 如图所示,两物体处于静止状态,它们的质量m1=2m2,它们与水平面间的动摩擦因数为μ2=2μ1,开始它们之间被细绳连接,并夹一压缩状态的轻质弹簧.当烧断细线后,两物体脱离弹簧时的速度均不为零,则下列结论正确的是( )
如图所示,两物体处于静止状态,它们的质量m1=2m2,它们与水平面间的动摩擦因数为μ2=2μ1,开始它们之间被细绳连接,并夹一压缩状态的轻质弹簧.当烧断细线后,两物体脱离弹簧时的速度均不为零,则下列结论正确的是( ) 如图所示,固定斜面的倾角θ=30°,物体A与斜面之间的动摩擦因数为μ=
如图所示,固定斜面的倾角θ=30°,物体A与斜面之间的动摩擦因数为μ= 如图所示,固定斜面的倾角θ=30°,物体A与斜面之间的动摩擦因数为
如图所示,固定斜面的倾角θ=30°,物体A与斜面之间的动摩擦因数为