题目内容
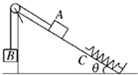 如图所示,固定斜面的倾角θ=30°,物体A与斜面之间的动摩擦因数为μ=
如图所示,固定斜面的倾角θ=30°,物体A与斜面之间的动摩擦因数为μ=
| ||
| 2 |
(1)物体A向下运动刚到C点时的速度;
(2)弹簧的最大压缩量;
(3)弹簧中的最大弹性势能.
分析:(1)物体A向下运动到C点的过程中,A的重力势能及AB的动能都减小,转化为B的重力势能和摩擦生热,根据能量守恒定律列式求出物体A向下运动刚到C点时的速度;
(2)从物体A接触弹簧到将弹簧压缩到最短后回到C点的过程中,弹簧的弹力和重力做功都为零,根据动能定理求出弹簧的最大压缩量;
(3)弹簧从压缩最短到恰好能弹到C点的过程中,根据能量守恒定律求解弹簧中的最大弹性势能.
(2)从物体A接触弹簧到将弹簧压缩到最短后回到C点的过程中,弹簧的弹力和重力做功都为零,根据动能定理求出弹簧的最大压缩量;
(3)弹簧从压缩最短到恰好能弹到C点的过程中,根据能量守恒定律求解弹簧中的最大弹性势能.
解答:解:(1)A和斜面间的滑动摩擦力大小为f=2μmgcosθ,物体A向下运动到C点的过程中,根据功能关系有:
2mgLsinθ+
?3mv02=
?3mv2+mgL+fL,
代入解得v=
.
(2)从物体A接触弹簧,将弹簧压缩到最短后又恰回到C点,对系统应用动能定理,
-f?2x=0-
×3mv2,解得x=
-
=
-
.
(3)弹簧从压缩最短到恰好能弹到C点的过程中,对系统根据能量关系有
Ep+mgx=2mgxsinθ+fx
因为mgx=2mgxsinθ
所以Ep=fx=
mv02-
μmgL=
mv02-
mgL.
答:
(1)物体A向下运动刚到C点时的速度为
;
(2)弹簧的最大压缩量为
-
;
(3)弹簧中的最大弹性势能为
mv02-
mgL.
2mgLsinθ+
| 1 |
| 2 |
| 1 |
| 2 |
代入解得v=
|
(2)从物体A接触弹簧,将弹簧压缩到最短后又恰回到C点,对系统应用动能定理,
-f?2x=0-
| 1 |
| 2 |
| ||
| 4μg |
| L |
| 2 |
| ||
| 2g |
| L |
| 2 |
(3)弹簧从压缩最短到恰好能弹到C点的过程中,对系统根据能量关系有
Ep+mgx=2mgxsinθ+fx
因为mgx=2mgxsinθ
所以Ep=fx=
| 3 |
| 4 |
| ||
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
答:
(1)物体A向下运动刚到C点时的速度为
|
(2)弹簧的最大压缩量为
| ||
| 2g |
| L |
| 2 |
(3)弹簧中的最大弹性势能为
| 3 |
| 4 |
| 3 |
| 4 |
点评:本题关键是搞清能量如何转化的,可以先分清在物体运动的过程中涉及几种形式的能量,分析哪些能量增加,哪些能量减小,再判断能量如何转化.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
 如图所示,固定斜面的倾角为30°,现用平行于斜面的力F拉着质量为m的物体沿斜面向上运动,物体的加速度大小为a,若该物体放在斜面上沿斜面下滑时的加速度大小也为a,则力F的大小是( )
如图所示,固定斜面的倾角为30°,现用平行于斜面的力F拉着质量为m的物体沿斜面向上运动,物体的加速度大小为a,若该物体放在斜面上沿斜面下滑时的加速度大小也为a,则力F的大小是( ) 如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求:
如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求: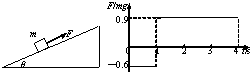 如图所示,固定斜面的倾角为θ=37°,物体与斜面间的动摩擦因数为μ=0.25,物体受到平行于斜面的力F作用静止开始运动,力F随时间t变化规律如图(以平行于斜面向上为正方向),前4s内物体运动的最大加速度大小为
如图所示,固定斜面的倾角为θ=37°,物体与斜面间的动摩擦因数为μ=0.25,物体受到平行于斜面的力F作用静止开始运动,力F随时间t变化规律如图(以平行于斜面向上为正方向),前4s内物体运动的最大加速度大小为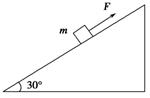
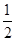 mg B.mg C.
mg B.mg C.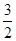 mg D.
mg D.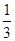 mg
mg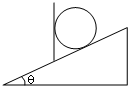 如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求:
如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求: