题目内容
3.如图所示,一条带有圆轨道的长轨道水平固定,圆轨道竖直,底端分别与两侧的直轨道相切,半径R=0.5m,物块A以V0=6m/s的速度滑入圆轨道,滑过最高点Q,再沿圆轨道滑出后,与直轨上P处静止的物块B碰撞,碰后粘在一起运动.P点左侧轨道光滑,右侧轨道呈粗糙段,光滑段交替排列,每段长度都为L=0.1m.物块与各粗糙段间的动摩擦因数都为μ=0.1,A、B的质量均为m=1kg(重力加速度g取10m/s2;A、B视为质点,碰撞时间极短).
(1)求A滑过Q点时的速度大小V和受到的弹力大小F;
(2)若碰后AB最终停止在第k个粗糙段上,求k的数值;
(3)求碰后AB滑至第n个(n<k)光滑段上的速度VAB与n的关系式.
分析 (1)由机械能守恒定律可求得A滑过Q点的速度,由向心力公式可求得弹力大小;
(2)由机械能守恒定律可求得AB碰撞前A的速度,再对碰撞过程由动量守恒定律可求得碰后的速度;则可求得总动能,再由摩擦力做功求出每段上消耗的机械能;即可求得比值;
(3)设总共经历了n段,根据每一段上消耗的能量,由能量守恒可求得表达式.
解答 解:(1)由机械能守恒定律可得:
$\frac{1}{2}$mv02=mg(2R)+$\frac{1}{2}$mv2;
解得:v=4m/s;
由F+mg=m$\frac{{v}^{2}}{R}$可得:
F=22N;
(2)AB碰撞前A的速度为vA,由机械能守恒定律可得:
$\frac{1}{2}$mv02=$\frac{1}{2}$mvA2
得vA=v0=6m/s;
AB碰撞后以共同速度vP前进,设向右为正方向,由动量守恒定律可得:
mv0=(m+m)vp
解得:vP=3m/s;
故总动能EK=$\frac{1}{2}$(m+m)vP2=$\frac{1}{2}$×2×9=9J;
滑块每经过一段粗糙段损失的机械能△EK=fL=μ(m+m)gL=0.1×20×0.1=0.2J;
k=$\frac{{E}_{k}}{△E}$=$\frac{9}{0.2}$=45;
(3)AB整体滑到第n个光滑段上损失的能量;
E损=nE=0.2nJ
从AB碰撞后运动到第n个光滑段的过程中,由能量守恒定律可得:
$\frac{1}{2}$(m+m)vP2-$\frac{1}{2}$(m+m)vAB2=n△E,
代入解得:vAB=$\sqrt{9-0.2n}$m/s;
答:1)A滑过Q点时的速度大小V为4m/s;受到的弹力大小F为22N;
(2)k的数值为45;
(3)碰后AB滑至第n个(n<k)光滑段上的速度VAB与n的关系式为vAB=$\sqrt{9-0.2n}$m/s;
点评 本题考查动量守恒定律、机械能守恒定律及向心力等内容,要求我们能正确分析物理过程,做好受力分析及能量分析;要注意能量的转化与守恒的灵活应用.

| A. | 气泡内气体对外做正功 | B. | 气泡的内气体的内能增大 | ||
| C. | 气泡内气体压强变大 | D. | 气泡内气体吸热全部用于对外做功 |
| A. | 探测器的质量越大,脱离星球所需要的发射速度越大 | |
| B. | 探测器在地球表面受到的引力比在火星表面的大 | |
| C. | 探测器分别脱离两星球所需要的发射速度相等 | |
| D. | 探测器脱离星球的过程中,势能逐渐增大 |
| A. | 200 | B. | 400 | C. | 1600 | D. | 3200 |
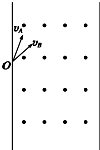 如图所示,带有正电荷的A粒子和B粒子同时以同样大小的速度从宽度为d的有界匀强磁场的边界上的O点分别以30°和60°(与边界的夹角)射入磁场,又恰好都不从另一边界飞出,则下列说法中正确的是( )
如图所示,带有正电荷的A粒子和B粒子同时以同样大小的速度从宽度为d的有界匀强磁场的边界上的O点分别以30°和60°(与边界的夹角)射入磁场,又恰好都不从另一边界飞出,则下列说法中正确的是( )| A. | A、B两粒子在磁场中做圆周运动的半径之比为1:$\sqrt{3}$ | |
| B. | A、B两粒子在磁场中做圆周运动的半径之比为3(2-$\sqrt{3}$):1 | |
| C. | A、B两粒子的$\frac{q}{m}$之比是$\sqrt{3}$:1 | |
| D. | A、B两粒子的$\frac{q}{m}$之比是1:$\sqrt{3}$ |
 如图所示,位于竖直平面内的粗糙斜轨道AB与光滑水平轨道BC及竖直光滑半圆形轨道CD平滑连接,半圆轨道的直径DC垂直于BC,斜轨道的倾角θ=37°,圆形轨道的半径为R.一质量为m的小滑块(可看作质点)从高为H的斜轨道上的P点由静止开始下滑,然后从直轨道进入圆形轨道运动,运动到圆形轨道的最高点D时对轨道的压力大小恰与重力相等,小滑块过最高点D后做平抛运动,恰好垂直撞击在斜轨道的Q点.已知sin37°=0.6,cos37°=0.8,重力加速度为g,求:
如图所示,位于竖直平面内的粗糙斜轨道AB与光滑水平轨道BC及竖直光滑半圆形轨道CD平滑连接,半圆轨道的直径DC垂直于BC,斜轨道的倾角θ=37°,圆形轨道的半径为R.一质量为m的小滑块(可看作质点)从高为H的斜轨道上的P点由静止开始下滑,然后从直轨道进入圆形轨道运动,运动到圆形轨道的最高点D时对轨道的压力大小恰与重力相等,小滑块过最高点D后做平抛运动,恰好垂直撞击在斜轨道的Q点.已知sin37°=0.6,cos37°=0.8,重力加速度为g,求:
 如图,轨道ABCD固定在竖直平面内,ABC段光滑,BC段是以O(A与O在同一直线上)为圆心,半径R=10m的圆弧管道,水平平台CD与圆弧管道下端C点相切,质量m=4kg的物块(可视为质点)以水平初速度v0=15m/s从A开始始终沿轨道运动,最后停留在D点,物块与CD间的动摩擦因数μ=0.25,取g=10m/s2,求:
如图,轨道ABCD固定在竖直平面内,ABC段光滑,BC段是以O(A与O在同一直线上)为圆心,半径R=10m的圆弧管道,水平平台CD与圆弧管道下端C点相切,质量m=4kg的物块(可视为质点)以水平初速度v0=15m/s从A开始始终沿轨道运动,最后停留在D点,物块与CD间的动摩擦因数μ=0.25,取g=10m/s2,求: