题目内容
11.质量为60kg的人,不慎从高空支架上跌落,由于弹性安全带的保护,使他悬挂在空中.已知安全带原长为5m,缓冲时间(从安全带伸直到速度减为0的时间)是1.2s,求安全带在1.2s内受到的平均冲力是多少?分析 根据机械能守恒定律求出安全带绷直时人的速度,再对缓冲的过程运用动量定理,求出平均冲力的大小.
解答 解:设物体自由落下5m时的速度为v,根据机械能守恒定律$mgh=\frac{1}{2}m{v^2}$,
得v=$\sqrt{2gh}=\sqrt{2×10×5}m/s=10m/s$
在安全带缓冲的过程中,以向下的方向为正方向,则
mgt2-Ft2=0-mv
解得平均拉力$F=\frac{{mg{t_2}+mv}}{t_2}=\frac{600×1.2+60×10}{1.2}N=1100N$.
答:安全带在1.2s内受到的平均冲力是1100N.
点评 本题考查了动量定理的基本运用,知道合力的冲量等于动量的变化,知道公式的矢量性,基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6. 如图所示,若套在条形磁铁上的闭合弹性金属导线圈由图示的Ⅰ位置缩小到图示Ⅱ位置,则在此过程中,关于线圈的感应电流及其方向(从上往下看)是( )
如图所示,若套在条形磁铁上的闭合弹性金属导线圈由图示的Ⅰ位置缩小到图示Ⅱ位置,则在此过程中,关于线圈的感应电流及其方向(从上往下看)是( )
 如图所示,若套在条形磁铁上的闭合弹性金属导线圈由图示的Ⅰ位置缩小到图示Ⅱ位置,则在此过程中,关于线圈的感应电流及其方向(从上往下看)是( )
如图所示,若套在条形磁铁上的闭合弹性金属导线圈由图示的Ⅰ位置缩小到图示Ⅱ位置,则在此过程中,关于线圈的感应电流及其方向(从上往下看)是( )| A. | 有顺时针方向的感应电流 | B. | 有逆时针方向的感应电流 | ||
| C. | 先逆时针后顺时针方向的感应电流 | D. | 无感应电流 |
3. 如图所示,一只半球形碗放在水平桌面上,碗的半径为R,质量为m的蚂蚁从碗底某一竖直面向上爬,当爬到离碗底R=$\frac{\sqrt{3}}{2}$R的高度时,会滑落到碗底,若最大静摩擦力等于滑动摩擦力,那么蚂蚁和碗面间的动摩擦因数为( )
如图所示,一只半球形碗放在水平桌面上,碗的半径为R,质量为m的蚂蚁从碗底某一竖直面向上爬,当爬到离碗底R=$\frac{\sqrt{3}}{2}$R的高度时,会滑落到碗底,若最大静摩擦力等于滑动摩擦力,那么蚂蚁和碗面间的动摩擦因数为( )
 如图所示,一只半球形碗放在水平桌面上,碗的半径为R,质量为m的蚂蚁从碗底某一竖直面向上爬,当爬到离碗底R=$\frac{\sqrt{3}}{2}$R的高度时,会滑落到碗底,若最大静摩擦力等于滑动摩擦力,那么蚂蚁和碗面间的动摩擦因数为( )
如图所示,一只半球形碗放在水平桌面上,碗的半径为R,质量为m的蚂蚁从碗底某一竖直面向上爬,当爬到离碗底R=$\frac{\sqrt{3}}{2}$R的高度时,会滑落到碗底,若最大静摩擦力等于滑动摩擦力,那么蚂蚁和碗面间的动摩擦因数为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{2}}{2}$ |

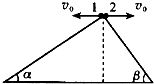 两高度相同的斜面,倾角分别为α、γ,小球1、2分别由斜面顶端以相同水平速度v0抛出,如图所示,假设两球能落在斜面上,则两球的
两高度相同的斜面,倾角分别为α、γ,小球1、2分别由斜面顶端以相同水平速度v0抛出,如图所示,假设两球能落在斜面上,则两球的 某同学在做“研究平抛运动”的实验中,做出了小球运动轨迹如图,A为抛出点的位置,求出物体做平抛运动的初速度为大小2m/s.(g取10m/s2)
某同学在做“研究平抛运动”的实验中,做出了小球运动轨迹如图,A为抛出点的位置,求出物体做平抛运动的初速度为大小2m/s.(g取10m/s2) 在距地面高H=45m处,有一小球A以初速度20m/s水平抛出,与此同时,在A的正下方有一物块B也以相同的初速度同方向滑出,B与地面间的动摩擦因数为0.5,A、B均可看作质点,空气阻力不计,求:
在距地面高H=45m处,有一小球A以初速度20m/s水平抛出,与此同时,在A的正下方有一物块B也以相同的初速度同方向滑出,B与地面间的动摩擦因数为0.5,A、B均可看作质点,空气阻力不计,求: