题目内容
6. 如图所示,长为L=6m、质量M=4kg的长木板放置于光滑的水平面上,其左端有一大小可忽略,质量为m=1kg的物块,物块与木板间的动摩擦因数为μ=0.4,开始时物块与木板都处于静止状态,现对物块施加方向水平向右的恒定拉力F作用,取g=10m/s2.
如图所示,长为L=6m、质量M=4kg的长木板放置于光滑的水平面上,其左端有一大小可忽略,质量为m=1kg的物块,物块与木板间的动摩擦因数为μ=0.4,开始时物块与木板都处于静止状态,现对物块施加方向水平向右的恒定拉力F作用,取g=10m/s2.(1)为使物块与木板发生相对滑动,恒定拉力至少为多少;
(2)若F=8N,求物块从木板左端运动到右端经历的时间;
(3)若F=8N,为使物块不从木板上滑离,求恒力F的最长作用时间.
分析 (1)对小物块和木板进行受力分析,根据牛顿第二定律求小物块的加速度;明确发生相对运动的条件是两物体之间恰好达到最大静摩擦力;
(2)小物块向右加速运动,长木板亦向右加速运动,两者位移差为木板长度时小物块到达木板的右端,根据位移时间关系求解即可.
(3)根据牛顿第二定律可求得二者的加速度,再根据二者达相对静止时的速度相等,根据位移公式进行列式,联立可求得恒力F作用的时间.
解答 解:
(1)设物块与木板恰好发生相对滑动时,拉力为F0,整体的加速度大小为a,则:
对整体:F0=(m+M)a
对木板:μmg=Ma
解得:F0=5N
即,为使物块与木板发生相对滑动,恒定拉力至少为5N;
(2)物块的加速度大小为:am=$\frac{F-μmg}{m}$
解得:am=4m/s2
木板的加速度大小为:aM=$\frac{μmg}{M}$
解得:aM=1m/s2
设物块滑到木板右端所需时间为t,则:$\frac{1}{2}$amt2-$\frac{1}{2}$aMt2=L
解之,得:t=2s
(3)设力F作用一段时间t1后撤去,撤去后经时间t2物块与木板相对静止;撤去力F后,木板的加速度不变,物块的加速度大小为:am′=μg=4 m/s2
两物体开始运动至相对静止过程:
物块的位移大小为:x=$\frac{1}{2}$amt12+amt1t2-$\frac{1}{2}$am′t22①
木板的位移大小为:X=$\frac{1}{2}$aM(t1+t2)2②
物块恰不滑离木板,满足:x-X=L③
根据速度关系,有:amt1-am′t2=aM(t1+t2)④
联立①②③④式,代入数据,得:t1=210 s
即为使物块不从木板上滑离,恒力F的最长作用时间为210 s
答:(1)为使物块与木板发生相对滑动,恒定拉力至少为5N;
(2)若F=8N,求物块从木板左端运动到右端经历的时间为2s;
(3)若F=8N,为使物块不从木板上滑离,恒力F的最长作用时间为210s.
点评 本题考查牛顿第二定律的综合应用,要注意明确涉及多个物体时,一定要注意正确进行受力分析,明确运动规律,找出两物体间的运动关系,联立方程求解.

 如图所示,物块P与Q的质量分别为m和2m,各接触面间的动摩擦因数均为μ,R为定滑轮,其质量及摩擦均可忽略不计,现用一水品拉力F作用于P上并使P、Q发生运动,则F至少为( )
如图所示,物块P与Q的质量分别为m和2m,各接触面间的动摩擦因数均为μ,R为定滑轮,其质量及摩擦均可忽略不计,现用一水品拉力F作用于P上并使P、Q发生运动,则F至少为( )| A. | 3μmg | B. | 4μmg | C. | 5μmg | D. | 6μmg |
 如图所示,河岸A处有一只小船.河宽为300m,水流速度为4m/s,在A点下游400m处有一瀑布.小船从A处开出后不能掉进瀑布且要到达对岸,船相对于水的最小速度为( )
如图所示,河岸A处有一只小船.河宽为300m,水流速度为4m/s,在A点下游400m处有一瀑布.小船从A处开出后不能掉进瀑布且要到达对岸,船相对于水的最小速度为( )| A. | 2m/s | B. | 2.4m/s | C. | 3m/s | D. | 3.5m/s |
 如图所示,光滑的水平地面上有质量均为m的a、b、c三个木块,a、c之间用轻质细绳连接(细绳水平).现用一个水平恒力F作用在b上,三者开始一起做匀加速运动,运动过程中把一块橡皮泥粘在某一木块上面,系统仍加速运动,且始终没有发生相对滑动.在粘上橡皮泥并达到稳定后,下列说法正确的是( )
如图所示,光滑的水平地面上有质量均为m的a、b、c三个木块,a、c之间用轻质细绳连接(细绳水平).现用一个水平恒力F作用在b上,三者开始一起做匀加速运动,运动过程中把一块橡皮泥粘在某一木块上面,系统仍加速运动,且始终没有发生相对滑动.在粘上橡皮泥并达到稳定后,下列说法正确的是( )| A. | 无论粘在哪个木块上面,系统的加速度都减小 | |
| B. | 若粘在a木块上面,则绳的张力减小,a、b间的摩擦力不变 | |
| C. | 若粘在b木块上面,则绳的张力和a、b间的摩擦力都减小 | |
| D. | 若粘在c木块上面,则绳的张力和a、b间的摩擦力都减小 |
| A. | 奥斯特在实验中观察到通电导线下方磁针的转动,发现了电流的磁效应 | |
| B. | 安培通过实验发现磁场对电流有作用力,此力的方向与磁场方向垂直 | |
| C. | 法拉第通过实验得出,“磁生电”是一种在运动或变化的过程中才能出现的效应 | |
| D. | 楞次在分析实验事实后提出,感应电流的磁场方向总是与引起感应电流的原磁场方向相同 |
| A. | ON | B. | 6N | C. | 12N | D. | 15N |
| A. | 0.25A方向顺流而下 | B. | 0.05A方向顺流而下 | ||
| C. | 0.25A方向逆流而上 | D. | 0.05A方向逆流而上 |
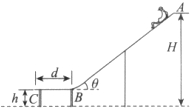 如图所示为水上滑梯的简化图,倾角θ=37°的斜滑道AB与水平滑道BC平滑连接,起点A距水面的高度H=4.0m,滑道末端C距水面的高度h=1.0m.玩耍的小孩从A处无初速滑下,从C处离开.将小孩视为质点,小孩与滑道各处的动摩擦因数μ=0.125,重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6,求:
如图所示为水上滑梯的简化图,倾角θ=37°的斜滑道AB与水平滑道BC平滑连接,起点A距水面的高度H=4.0m,滑道末端C距水面的高度h=1.0m.玩耍的小孩从A处无初速滑下,从C处离开.将小孩视为质点,小孩与滑道各处的动摩擦因数μ=0.125,重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6,求: