题目内容
14. 如图所示,一个质量为M,半径为R的光滑均质半球,静置于光滑水平桌面上,在球顶有一个质量为m的质点,由静止开始沿球面下滑,试求:质点离开球面以前的轨迹.
如图所示,一个质量为M,半径为R的光滑均质半球,静置于光滑水平桌面上,在球顶有一个质量为m的质点,由静止开始沿球面下滑,试求:质点离开球面以前的轨迹.
分析 质点下滑,半球后退,水平方向受到的外力为零,满足水平方向动量守恒,根据动量守恒定律求出小球水平位移的表达式,再根据几何关系求出竖直方向位移的表达式,从而求出轨迹方程.
解答  解:质点下滑,半球后退,水平方向合力为零,满足水平方向动量守恒,
解:质点下滑,半球后退,水平方向合力为零,满足水平方向动量守恒,
建立一个坐标:以半球球心O为原点,沿质点滑下一侧的水平轴为x坐标、竖直轴为y坐标.
由于质点相对半球总是做圆周运动的(离开球面前),引入相对运动中半球球心O′的方位角θ来表达质点的瞬时位置,如图所示:
设质点水平方向运动的位移为x,半圆运动的位移为X,运动时间为t,根据水平方向动量守恒定律得:
$M\frac{X}{t}=m\frac{x}{t}$,
根据几何关系得:
x+X=Rsinθ
解得:x=$\frac{M}{M+m}Rsinθ$…①
而由图知:y=Rcosθ…②
由①②得:
$\frac{{x}^{2}}{(\frac{MR}{M+m})^{2}}+\frac{{y}^{2}}{{R}^{2}}=1$
则质点的轨迹是一个长、短半轴分别为R和$\frac{M}{M+m}$R的椭圆.
答:质点离开球面以前的轨迹方程为$\frac{{x}^{2}}{{(\frac{MR}{M+m})}^{2}}+\frac{{y}^{2}}{{R}^{2}}=1$,轨迹是一个长、短半轴分别为R和$\frac{M}{M+m}$R的椭圆.
点评 解答本题的关键是掌握动量守恒定律的直接应用,知道在运动过程中,水平方向的动量是守恒的,同时注意几何关系在解题时的应用,难度较大.

练习册系列答案
相关题目
4.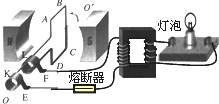 如图所示,50匝矩形闭合导线框ABCD处于磁感应强度大小B=$\frac{\sqrt{2}}{10}$T的水平匀强磁场中,线框面积S=0.5m2,线框电阻不计.线框绕垂直于磁场的轴OO′以角速度ω=200rad/s匀速转动,并与理想变压器原线圈相连,副线圈接入一只“220V,60W”灯泡,且灯泡正常发光,熔断器允许通过的最大电流为10A,下列说法正确的是( )
如图所示,50匝矩形闭合导线框ABCD处于磁感应强度大小B=$\frac{\sqrt{2}}{10}$T的水平匀强磁场中,线框面积S=0.5m2,线框电阻不计.线框绕垂直于磁场的轴OO′以角速度ω=200rad/s匀速转动,并与理想变压器原线圈相连,副线圈接入一只“220V,60W”灯泡,且灯泡正常发光,熔断器允许通过的最大电流为10A,下列说法正确的是( )
 如图所示,50匝矩形闭合导线框ABCD处于磁感应强度大小B=$\frac{\sqrt{2}}{10}$T的水平匀强磁场中,线框面积S=0.5m2,线框电阻不计.线框绕垂直于磁场的轴OO′以角速度ω=200rad/s匀速转动,并与理想变压器原线圈相连,副线圈接入一只“220V,60W”灯泡,且灯泡正常发光,熔断器允许通过的最大电流为10A,下列说法正确的是( )
如图所示,50匝矩形闭合导线框ABCD处于磁感应强度大小B=$\frac{\sqrt{2}}{10}$T的水平匀强磁场中,线框面积S=0.5m2,线框电阻不计.线框绕垂直于磁场的轴OO′以角速度ω=200rad/s匀速转动,并与理想变压器原线圈相连,副线圈接入一只“220V,60W”灯泡,且灯泡正常发光,熔断器允许通过的最大电流为10A,下列说法正确的是( )| A. | 中性面位置穿过线框的磁通量为零 | |
| B. | 线框中产生交变电压的有效值为500$\sqrt{2}$V | |
| C. | 变压器原、副线圈匝数之比为25:22 | |
| D. | 允许变压器输出的最大功率为5000W |
 用如图所示装置可验证机械能守恒定律.轻绳两端系着质量相等的物块A、B,物块B上放置一金属片C.铁架台上固定一金属圆环,圆环处在物块B正下方.系统静止时,金属片C与圆环间的高度差为h.由此释放B,系统开始运动,当物块B穿过圆环时,金属片C被搁置在圆环上.两光电门固定在铁架台上的P1、P2处,通过数字计时器可测出物块B通过P1、P2这段距离的时间.
用如图所示装置可验证机械能守恒定律.轻绳两端系着质量相等的物块A、B,物块B上放置一金属片C.铁架台上固定一金属圆环,圆环处在物块B正下方.系统静止时,金属片C与圆环间的高度差为h.由此释放B,系统开始运动,当物块B穿过圆环时,金属片C被搁置在圆环上.两光电门固定在铁架台上的P1、P2处,通过数字计时器可测出物块B通过P1、P2这段距离的时间. 如图所示,一个$\frac{1}{4}$透明球体放置在水平面上,一束蓝光从A点沿水平方向射入球体后经B点射出,最后射到水平面上的C点.已知∠BOC=30°,∠BCO=30°,该球体对蓝光的折射率为$\sqrt{3}$;若换用一束红光同样从A点水平射向该球体,则它从球体射出后落到水平面上形成的光点与C点相比,位置偏右(填“偏左”、“偏右”或“不变”).
如图所示,一个$\frac{1}{4}$透明球体放置在水平面上,一束蓝光从A点沿水平方向射入球体后经B点射出,最后射到水平面上的C点.已知∠BOC=30°,∠BCO=30°,该球体对蓝光的折射率为$\sqrt{3}$;若换用一束红光同样从A点水平射向该球体,则它从球体射出后落到水平面上形成的光点与C点相比,位置偏右(填“偏左”、“偏右”或“不变”).

 如图所示,光滑水平桌面上开一个光滑小孔,从孔中穿一根细绳,绳一端系一个小球,另一端用力F1向下拉,以维持小球在光滑水平面上做半径为R1的匀速圆周运动,今改变拉力,当大小变为F2,使小球仍在水平面上做匀速圆周运动,但半径变为R2,小球运动半径由R1变为R2过程中拉力对小球做的功多大?
如图所示,光滑水平桌面上开一个光滑小孔,从孔中穿一根细绳,绳一端系一个小球,另一端用力F1向下拉,以维持小球在光滑水平面上做半径为R1的匀速圆周运动,今改变拉力,当大小变为F2,使小球仍在水平面上做匀速圆周运动,但半径变为R2,小球运动半径由R1变为R2过程中拉力对小球做的功多大? 质量为m=2kg的两平板车M和N靠在一起且静止在光滑水平面上,两平板车的上表面在同一高度且表面粗糙,在M车的左端静止着质量为mA=2kg的物体A(可视为质点),如图所示,一颗质量为mB=20g的子弹以800m/s的水平速度射穿A后,速度变为100m/s,当物体A从M车滑到N车上时,M车与N车立即分开,最后物体A与N车具有相同的速度vAN=3m/s,求物体A在M车的左端和右端的速度分别是多大.
质量为m=2kg的两平板车M和N靠在一起且静止在光滑水平面上,两平板车的上表面在同一高度且表面粗糙,在M车的左端静止着质量为mA=2kg的物体A(可视为质点),如图所示,一颗质量为mB=20g的子弹以800m/s的水平速度射穿A后,速度变为100m/s,当物体A从M车滑到N车上时,M车与N车立即分开,最后物体A与N车具有相同的速度vAN=3m/s,求物体A在M车的左端和右端的速度分别是多大.