题目内容
6. 如图,直角坐标系xOy中,A、C分别为x、y轴上的两点,OC长为L,∠OAC=30°,△OAC区域内有垂直于xOy平面向外的匀强磁场,区域外无磁场,有大量质量为m、电荷量为q的带正电粒子,以平行于y轴方向从OA边各处持续不断射入磁场,已知能从AC边垂直射出的粒子在磁场中的运动时间为t,不考虑粒子间的相互作用且粒子重力不计.
如图,直角坐标系xOy中,A、C分别为x、y轴上的两点,OC长为L,∠OAC=30°,△OAC区域内有垂直于xOy平面向外的匀强磁场,区域外无磁场,有大量质量为m、电荷量为q的带正电粒子,以平行于y轴方向从OA边各处持续不断射入磁场,已知能从AC边垂直射出的粒子在磁场中的运动时间为t,不考虑粒子间的相互作用且粒子重力不计.(1)求磁场磁感应强度B的大小;
(2)有些粒子的运动轨迹会与AC边相切,求相切轨迹的最大半径rm及其对应的入射速度vm;
(3)若粒子入射速度相同,有些粒子能在边界AC上相遇,求相遇的粒子入射时间差的最大值.
分析 (1)由题设条件,已知垂直于AC边射出的粒子在磁场中的时间为t,显然,其偏转角为90°,根据周期公式就能求出磁感应强度大小.
(2)显然与AC相切的最大半径是从O点出发的粒子,画出其运动轨迹,由几何关系求出半径,由洛仑兹力提供向心力从而求出最大速度.
(3)由于入射速度相同,则半径一样,能在AC边相遇的情形有多种,两圆弧对应的圆心角之差△θ最大时,两粒子入射的时间差最大.由分析知道:当两个粒子轨迹圆心与AC上相遇点构成等边三角形时,两个粒子相遇的时间差最大.
解答  解:(1)恰恰好垂直于AC边射出磁场的轨迹如图,根据几何知识得,在磁场
解:(1)恰恰好垂直于AC边射出磁场的轨迹如图,根据几何知识得,在磁场
中的轨迹对应的圆心角θ=30°,在磁场中的运动时间:
t=$\frac{θ}{360°}T$
又T=$\frac{2πm}{qB}$
得到:B=$\frac{πm}{6qt}$
(2)从O点入射的粒子精悍AC边相切时半径最大,根据几何关系得:
rm+$\frac{{r}_{m}}{sin30°}=\frac{L}{tan30°}$
根据牛顿第二定律得:$q{v}_{m}B=m\frac{{{v}_{m}}^{2}}{{r}_{m}}$
所以rm=$\frac{\sqrt{3}L}{3}$
vm=$\frac{\sqrt{3}πL}{18t}$
(3)由于入射速度相同,则半径一样,能在AC边相遇的情形有多种,两
圆弧对应的圆心角之差△θ最大时,两粒子入射的时间差最大.如图甲,
△O1BO2为等腰三角形,由几何关系得:
△θ=θ1-θ2=∠O1BO2
又θ1+θ2=180°
得△θ=2θ1-180°
可见:θ1最大时,△θ最大.
而当B为切点时,θ1最大(如图乙),△O1BO2为等边三角形,由几何关系得:
△θ=60°
则$△{t}_{max}=\frac{△θ}{360°}T=\frac{1}{6}×\frac{2πm}{q×\frac{πm}{6qt}}=2t$
答:(1)磁场磁感应强度B的大小为$\frac{πm}{6qt}$.
(2)有些粒子的运动轨迹会与AC边相切,相切轨迹的最大半径rm及其对应的入射速度vm为$\frac{\sqrt{3}πL}{18t}$.
(3)若粒子入射速度相同,有些粒子能在边界AC上相遇,相遇的粒子入射时间差的最大值为2t.
点评 该题是纯粹的带电粒子在磁场中以相同的方向进入三角形区域做匀速圆周运动的特例,其不同之处在于第三问的相遇问题且求相遇的最大时间差,要找到此种情况的情形,画出两个粒子的轨迹图,由周期公式能求出最大时间差.

| A. | 强相互作用力是原子核内部的力,弱相互作用力是原子核外部的力 | |
| B. | 强相互作用力和弱相互作用力都是短程力,其力程均在10-18米范围内 | |
| C. | 每个核子只跟邻近的核子发生核力作用,这种性质称为核力的饱和性 | |
| D. | 组成原子核的核子越多,它的结合能越低 |
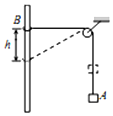 如图所示,物块A和圆环B用绕过定滑轮的轻绳连接在一起,圆环B套在光滑的竖直固定杆上,开始时连接B的绳子处于水平.零时刻由静止释放B,经时间t,B下降h,此时,速度达到最大.不计滑轮摩擦和空气的阻力,则( )
如图所示,物块A和圆环B用绕过定滑轮的轻绳连接在一起,圆环B套在光滑的竖直固定杆上,开始时连接B的绳子处于水平.零时刻由静止释放B,经时间t,B下降h,此时,速度达到最大.不计滑轮摩擦和空气的阻力,则( )| A. | t时刻B的速度大于A的速度 | |
| B. | t时刻B的加速度最大 | |
| C. | 0~t过程A的机械能增加量小于B的机械能减小量 | |
| D. | 0~t过程绳拉力对物块B做的功在数值上等于物块B机械能的减少量 |
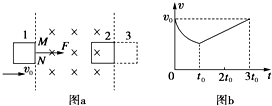
| A. | t=0时,线框右侧边MN的两端电压为Bav0 | |
| B. | 在t0时刻线框的速度为${v_0}-\frac{{F{t_0}}}{m}$ | |
| C. | 线框完全离开磁场的瞬间(位置3)的速度一定比t0时刻线框的速度大 | |
| D. | 线框从进入磁场(位置1)到完全离开磁场(位置3)的过程中产生的电热为2Fb |
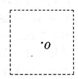 科研人员常用磁场来约束运动的带电粒子,如图所示,粒子源位于纸面内一边长为a的正方形中心O处,可以沿纸面向各个方向发射速度不同的粒子,粒子质量为m、电荷量为q、最大速度为v,忽略粒子重力及粒子间相互作用,要使粒子均不能射出正方形区域,可在此区域加一垂直纸面的匀强磁场,则磁感应强度B的最小值为( )
科研人员常用磁场来约束运动的带电粒子,如图所示,粒子源位于纸面内一边长为a的正方形中心O处,可以沿纸面向各个方向发射速度不同的粒子,粒子质量为m、电荷量为q、最大速度为v,忽略粒子重力及粒子间相互作用,要使粒子均不能射出正方形区域,可在此区域加一垂直纸面的匀强磁场,则磁感应强度B的最小值为( )| A. | $\frac{2mv}{qa}$ | B. | $\frac{2\sqrt{2}mv}{qa}$ | C. | $\frac{4mv}{qa}$ | D. | $\frac{4\sqrt{2}mv}{qa}$ |
 高度为H=2m圆柱形容器中盛满折射率n=$\sqrt{2}$的某种透明液体,容器直径L=3m,在圆心O点正上方h高度处有一点光源S.
高度为H=2m圆柱形容器中盛满折射率n=$\sqrt{2}$的某种透明液体,容器直径L=3m,在圆心O点正上方h高度处有一点光源S. 如图所示,两根电阻不计,相距L足够长的平行金属直角导轨,一部分处于水平面内,另一部分在竖直平面内,导轨所在空间存在大小为B、方向竖直向下的匀强磁场,金属棒ab质量为2m,电阻为R,cd质量为m,电阻为2R,两棒与导轨间动摩擦因数均为μ,ab棒在水平向左拉力作用下,由静止开始沿水平轨道做匀加速运动,同时cd棒由静止释放,cd棒速度从0达到最大的过程中拉力做功为W,重力加速度为g,求:
如图所示,两根电阻不计,相距L足够长的平行金属直角导轨,一部分处于水平面内,另一部分在竖直平面内,导轨所在空间存在大小为B、方向竖直向下的匀强磁场,金属棒ab质量为2m,电阻为R,cd质量为m,电阻为2R,两棒与导轨间动摩擦因数均为μ,ab棒在水平向左拉力作用下,由静止开始沿水平轨道做匀加速运动,同时cd棒由静止释放,cd棒速度从0达到最大的过程中拉力做功为W,重力加速度为g,求: