题目内容
14. 高度为H=2m圆柱形容器中盛满折射率n=$\sqrt{2}$的某种透明液体,容器直径L=3m,在圆心O点正上方h高度处有一点光源S.
高度为H=2m圆柱形容器中盛满折射率n=$\sqrt{2}$的某种透明液体,容器直径L=3m,在圆心O点正上方h高度处有一点光源S.①从液面上方观察,要使S发出的光照亮整个液表,h应满足什么条件?
②若处在某位置时S发出的光恰好照亮整个液面,从光源S的正上方观察,该光源看上去距离液面的深度为多少?
分析 ①作出光路图,抓住临界情况,结合几何关系,运用sinC=$\frac{1}{n}$得出h的临界值,从而得出h的范围.
②根据光源S到水面的实际深度的临界值,结合${h}_{视}=\frac{{h}_{实}}{n}$求出光源看上去距离液面的深度.
解答 解:① 作出光路图,如图所示,当光在边缘恰好发生全反射时,
作出光路图,如图所示,当光在边缘恰好发生全反射时,
有:sinC=$\frac{1}{n}$,
又sinC=$\frac{\frac{L}{2}}{\sqrt{\frac{{L}^{2}}{4}+(H-h)^{2}}}$,
代入数据解得h=0.5m,
可知当h≤0.5m时,S发出的光照亮整个液表.
②若处在某位置时S发出的光恰好照亮整个液面,则h=0.5m,
则光源看上去距离液面的深度h′=$\frac{H-h}{n}=\frac{2-0.5}{\sqrt{2}}$m=$\frac{3\sqrt{2}}{4}$m.
答:①从液面上方观察,要使S发出的光照亮整个液表,h≤0.5m;
②若处在某位置时S发出的光恰好照亮整个液面,从光源S的正上方观察,该光源看上去距离液面的深度为$\frac{3\sqrt{2}}{4}$m.
点评 本题是几何光学中范围问题,关键是作出边界光线,根据折射定律和几何知识求解.

练习册系列答案
相关题目
5. 氢原子光谱在可见光部分只有四条谱线,一条红色、一条蓝色、两条紫色,它们分别是从n=3、4、5、6 能级向n=2能级跃迁时产生的,则( )
氢原子光谱在可见光部分只有四条谱线,一条红色、一条蓝色、两条紫色,它们分别是从n=3、4、5、6 能级向n=2能级跃迁时产生的,则( )
 氢原子光谱在可见光部分只有四条谱线,一条红色、一条蓝色、两条紫色,它们分别是从n=3、4、5、6 能级向n=2能级跃迁时产生的,则( )
氢原子光谱在可见光部分只有四条谱线,一条红色、一条蓝色、两条紫色,它们分别是从n=3、4、5、6 能级向n=2能级跃迁时产生的,则( )| A. | 红色光谱是氢原子从n=3能级向n=2能级跃迁时产生的 | |
| B. | 蓝色光谱是氢原子从n=6能级或n=5能级向n=2能级跃迁时产生的 | |
| C. | 若从n=6能级向n=1能级跃迁时,则能够产生红外线 | |
| D. | 若原子从n=4能级向n=2能级跃迁时,所产生的辐射不能使某金属发生光电效应,则原子从n=6能级向n=3能级跃迁时也不可能使该金属发生光电效应 |
2. 信息技术的高速发展,网络购物已经普及到人们的生活中.在某物流公司的货物常常用到如图所示的装置,两根完全相同、轴线在同一水平面内的平行长圆柱上放一均匀木板,木板的重心与两 圆柱等距,其中圆柱的半径 r=2cm,木板质量 m=5kg,木板与圆柱间的动摩擦因数μ=0.2,两圆柱以 角速度ω 绕轴线作相反方向的转动.现施加一过木板重心且平行圆柱轴线的拉力 F 于木板上,使其以速度 v=0.6m/s 沿圆柱表面做匀速运动.取 g=10m/s.下列说法中正确的是( )
信息技术的高速发展,网络购物已经普及到人们的生活中.在某物流公司的货物常常用到如图所示的装置,两根完全相同、轴线在同一水平面内的平行长圆柱上放一均匀木板,木板的重心与两 圆柱等距,其中圆柱的半径 r=2cm,木板质量 m=5kg,木板与圆柱间的动摩擦因数μ=0.2,两圆柱以 角速度ω 绕轴线作相反方向的转动.现施加一过木板重心且平行圆柱轴线的拉力 F 于木板上,使其以速度 v=0.6m/s 沿圆柱表面做匀速运动.取 g=10m/s.下列说法中正确的是( )
 信息技术的高速发展,网络购物已经普及到人们的生活中.在某物流公司的货物常常用到如图所示的装置,两根完全相同、轴线在同一水平面内的平行长圆柱上放一均匀木板,木板的重心与两 圆柱等距,其中圆柱的半径 r=2cm,木板质量 m=5kg,木板与圆柱间的动摩擦因数μ=0.2,两圆柱以 角速度ω 绕轴线作相反方向的转动.现施加一过木板重心且平行圆柱轴线的拉力 F 于木板上,使其以速度 v=0.6m/s 沿圆柱表面做匀速运动.取 g=10m/s.下列说法中正确的是( )
信息技术的高速发展,网络购物已经普及到人们的生活中.在某物流公司的货物常常用到如图所示的装置,两根完全相同、轴线在同一水平面内的平行长圆柱上放一均匀木板,木板的重心与两 圆柱等距,其中圆柱的半径 r=2cm,木板质量 m=5kg,木板与圆柱间的动摩擦因数μ=0.2,两圆柱以 角速度ω 绕轴线作相反方向的转动.现施加一过木板重心且平行圆柱轴线的拉力 F 于木板上,使其以速度 v=0.6m/s 沿圆柱表面做匀速运动.取 g=10m/s.下列说法中正确的是( )| A. | 若ω=0,则水平拉力 F=20N | |
| B. | 若ω=40rad/s,则水平拉力 F=6N | |
| C. | 若ω=40rad/s,木板移动距离 x=0.5m,则拉力所做的功为 4J | |
| D. | 不论ω 为多大,所需水平拉力恒为 10N |
3.许多科学家对物理学的发展做出了巨大贡献,下列说法中正确的是( )
| A. | 牛顿发现了万有引力定律后,用实验的方法测出了引力常量G的数值 | |
| B. | 伽利略用理想实验证明了力是维持物体运动的原因 | |
| C. | 赫兹用实验证明了电磁波的存在 | |
| D. | 楞次总结得出了感应电流的产生条件 | |
| E. | 麦克斯韦从理论上预言了电磁波的存在 | |
| F. | 卢瑟福根据α粒子散射实验现象提出了原子的核式结构模型 | |
| G. | 卡文迪许利用扭秤测出了静电力常量k的数值 |
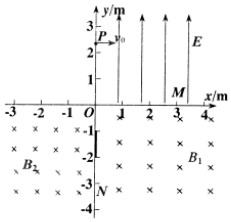 如图所示,在平面直角坐标系xOy内,第一象限存在沿y轴正方向的匀强电场E,第四象限存在一匀强磁场B1,第三象限存在一匀强磁场B2,一带负电粒子,从y轴上一点p(0,$\frac{3\sqrt{3}}{2}$)沿x轴正方向射出,一段时间后经x轴上点M(3,0)进入第四象限,经点N(0,-3)穿过y轴,已知粒子在p点初速度v0=2×106m/s,粒子比荷$\frac{q}{m}$=3×106C/Kg,求:
如图所示,在平面直角坐标系xOy内,第一象限存在沿y轴正方向的匀强电场E,第四象限存在一匀强磁场B1,第三象限存在一匀强磁场B2,一带负电粒子,从y轴上一点p(0,$\frac{3\sqrt{3}}{2}$)沿x轴正方向射出,一段时间后经x轴上点M(3,0)进入第四象限,经点N(0,-3)穿过y轴,已知粒子在p点初速度v0=2×106m/s,粒子比荷$\frac{q}{m}$=3×106C/Kg,求: 一圆环状玻璃砖截面如图所示,其内、外环半径分别为a、b且$\frac{a}{b}$=$\frac{\sqrt{3}}{3}$,一单色光以i=60°的入射角射入玻璃砖经一次反射后恰能沿原方向射出玻璃砖.
一圆环状玻璃砖截面如图所示,其内、外环半径分别为a、b且$\frac{a}{b}$=$\frac{\sqrt{3}}{3}$,一单色光以i=60°的入射角射入玻璃砖经一次反射后恰能沿原方向射出玻璃砖. 如图,直角坐标系xOy中,A、C分别为x、y轴上的两点,OC长为L,∠OAC=30°,△OAC区域内有垂直于xOy平面向外的匀强磁场,区域外无磁场,有大量质量为m、电荷量为q的带正电粒子,以平行于y轴方向从OA边各处持续不断射入磁场,已知能从AC边垂直射出的粒子在磁场中的运动时间为t,不考虑粒子间的相互作用且粒子重力不计.
如图,直角坐标系xOy中,A、C分别为x、y轴上的两点,OC长为L,∠OAC=30°,△OAC区域内有垂直于xOy平面向外的匀强磁场,区域外无磁场,有大量质量为m、电荷量为q的带正电粒子,以平行于y轴方向从OA边各处持续不断射入磁场,已知能从AC边垂直射出的粒子在磁场中的运动时间为t,不考虑粒子间的相互作用且粒子重力不计. 如图所示,直线ab是电场线中的一条电场线,从a点无初速度释放一电子,电子仅在电场力的作用下,沿直线从a点运动到b点,其电势能EP随位移x变化的规律如图乙所示.设a,b两点的电场强度大小分别为EA和EB,电势分别为φA和φB.则( )
如图所示,直线ab是电场线中的一条电场线,从a点无初速度释放一电子,电子仅在电场力的作用下,沿直线从a点运动到b点,其电势能EP随位移x变化的规律如图乙所示.设a,b两点的电场强度大小分别为EA和EB,电势分别为φA和φB.则( )