题目内容
2. 如图所示,如果把水星和金星绕太阳的运动视为匀速圆周运动,从水星与金星在一条直线上开始计时,若天文学家测得在相同时间内水星转过的角度为θ1,金星转过的角度为θ2(θ1、θ2均为锐角),则由此条件可求得( )
如图所示,如果把水星和金星绕太阳的运动视为匀速圆周运动,从水星与金星在一条直线上开始计时,若天文学家测得在相同时间内水星转过的角度为θ1,金星转过的角度为θ2(θ1、θ2均为锐角),则由此条件可求得( )| A. | 水星和金星绕太阳运动的周期之比 | |
| B. | 水星和金星的密度之比 | |
| C. | 水星和金星到太阳的距离之比 | |
| D. | 水星和金星绕太阳运动的向心加速度大小之比 |
分析 根据相同时间内转过的角度之比求出角速度之比,从而得出周期之比,根据万有引力提供向心力得出轨道半径和周期的关系,结合周期之比求出轨道半径之比.根据万有引力提供向心力得出向心加速度之比.
解答 解:A、相同时间内水星转过的角度为θ1;金星转过的角度为θ2,可知它们的角速度之比为θ1:θ2.周期T=$\frac{2π}{ω}$,则周期比为θ2:θ1.故A正确.
B、水星和金星是环绕天体,无法求出质量,也无法知道它们的半径,所以求不出密度比.故B错误.
C、根据$G\frac{Mm}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$得,$r=\root{3}{\frac{GM{T}^{2}}{4{π}^{2}}}$,周期之比可以得出,则可以得出水星和金星到太阳的距离之比,故C正确.
D、由于轨道半径之比可以得出,根据a=$r\frac{4{π}^{2}}{{T}^{2}}$,可以得出水星和金星绕太阳运动的向心加速度大小之比,故D正确.
故选:ACD.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,并能灵活运用,知道运用该理论只能求解中心天体质量,不能求解环绕天体质量.

练习册系列答案
相关题目
10.一物体在某行星表面受到的万有引力是它在地球表面受到的万有引力的$\frac{1}{9}$,在地球上走得很准的摆钟搬到此行星上后,此钟的分针走一整圈所经历的时间实际是( )
| A. | $\frac{1}{4}$h | B. | $\frac{1}{3}$h | C. | 3h | D. | 4h |
17.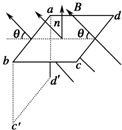 如图所示,面积为S的矩形导线框abcd,处在磁感应强度为B的匀强磁场中,磁场方向与线框平面成θ角.当线框从图示位置以ab为轴顺时针匀速转90°过程中,下列判断正确的是( )
如图所示,面积为S的矩形导线框abcd,处在磁感应强度为B的匀强磁场中,磁场方向与线框平面成θ角.当线框从图示位置以ab为轴顺时针匀速转90°过程中,下列判断正确的是( )
 如图所示,面积为S的矩形导线框abcd,处在磁感应强度为B的匀强磁场中,磁场方向与线框平面成θ角.当线框从图示位置以ab为轴顺时针匀速转90°过程中,下列判断正确的是( )
如图所示,面积为S的矩形导线框abcd,处在磁感应强度为B的匀强磁场中,磁场方向与线框平面成θ角.当线框从图示位置以ab为轴顺时针匀速转90°过程中,下列判断正确的是( )| A. | 线框中电流先减小后增大 | |
| B. | 线框中电流先增大后减小 | |
| C. | 线框中电流方向一直为a→b→c→d→a | |
| D. | 线框中电流方向先为a→b→c→d→a,再为a→d→c→b→a |
11. 如图所示,曲面PC和斜面PD固定在水平面MN上,C、D处平滑连接,O点位于斜面顶点P的正下方.某物体(可视为质点)从顶端P由静止开始分别沿曲面和斜面滑下,经过C、D两点后继续运动,最后停在水平面上的A、B两处.各处材质相同,忽略空气阻力,则( )
如图所示,曲面PC和斜面PD固定在水平面MN上,C、D处平滑连接,O点位于斜面顶点P的正下方.某物体(可视为质点)从顶端P由静止开始分别沿曲面和斜面滑下,经过C、D两点后继续运动,最后停在水平面上的A、B两处.各处材质相同,忽略空气阻力,则( )
 如图所示,曲面PC和斜面PD固定在水平面MN上,C、D处平滑连接,O点位于斜面顶点P的正下方.某物体(可视为质点)从顶端P由静止开始分别沿曲面和斜面滑下,经过C、D两点后继续运动,最后停在水平面上的A、B两处.各处材质相同,忽略空气阻力,则( )
如图所示,曲面PC和斜面PD固定在水平面MN上,C、D处平滑连接,O点位于斜面顶点P的正下方.某物体(可视为质点)从顶端P由静止开始分别沿曲面和斜面滑下,经过C、D两点后继续运动,最后停在水平面上的A、B两处.各处材质相同,忽略空气阻力,则( )| A. | 此物体在曲面PC和斜面PD上克服摩擦力做功一定相等 | |
| B. | 此物体沿PCA和沿PDB运动克服摩擦力做功一定相等 | |
| C. | 距离OA一定等于OB | |
| D. | 距离OA一定小于OB |
12.物体做直线运动,仅受力F的作用,且力F和速度同方向,在力F逐渐减小的过程中物体的运动情况是( )
| A. | 速度减小 | B. | 速度增大 | C. | 加速度变大 | D. | 加速度减小 |

 某同学为了测量某阻值约为5Ω的金属棒的电阻率,进行了如下操作,分别使用10分度游标卡尺和螺旋测微器测量金属棒的长度L和直径d,某次测量的示数如图1和图2所示,长度L=23.5mm,直径d=6.713mm
某同学为了测量某阻值约为5Ω的金属棒的电阻率,进行了如下操作,分别使用10分度游标卡尺和螺旋测微器测量金属棒的长度L和直径d,某次测量的示数如图1和图2所示,长度L=23.5mm,直径d=6.713mm 质量m=4Kg的物体静止在水平长木板上,如图甲所示,则:
质量m=4Kg的物体静止在水平长木板上,如图甲所示,则: