题目内容
4. 如图所示是倾角θ=37°的固定光滑斜面,两端有垂直于斜面的固定挡板P、Q,PQ距离L=2m,质量M=1.0kg的木块A(可看成质点)放在质量m=0.5kg的长d=0.8m的木板B上并一起停靠在挡板P处,A木块与斜面顶端的电动机间用平行于斜面不可伸长的轻绳相连接,现给木块A沿斜面向上的初速度,同时开动电动机保证木块A一直以初速度v0=1.6m/s沿斜面向上做匀速直线运动,已知木块A的下表面与木板B间动摩擦因数μ1=0.5,经过时间t,当B板右端到达Q处时刻,立刻关闭电动机,同时锁定A、B物体此时的位置.然后将A物体上下面翻转,使得A原来的上表面与木板B接触,已知翻转后的A、B接触面间的动摩擦因数变为μ2=0.25,且连接A与电动机的绳子仍与斜面平行.现在给A向下的初速度v1=2m/s,同时释放木板B,并开动电动机保证A木块一直以v1沿斜面向下做匀速直线运动,直到木板B与挡板P接触时关闭电动机并锁定A、B位置.求:
如图所示是倾角θ=37°的固定光滑斜面,两端有垂直于斜面的固定挡板P、Q,PQ距离L=2m,质量M=1.0kg的木块A(可看成质点)放在质量m=0.5kg的长d=0.8m的木板B上并一起停靠在挡板P处,A木块与斜面顶端的电动机间用平行于斜面不可伸长的轻绳相连接,现给木块A沿斜面向上的初速度,同时开动电动机保证木块A一直以初速度v0=1.6m/s沿斜面向上做匀速直线运动,已知木块A的下表面与木板B间动摩擦因数μ1=0.5,经过时间t,当B板右端到达Q处时刻,立刻关闭电动机,同时锁定A、B物体此时的位置.然后将A物体上下面翻转,使得A原来的上表面与木板B接触,已知翻转后的A、B接触面间的动摩擦因数变为μ2=0.25,且连接A与电动机的绳子仍与斜面平行.现在给A向下的初速度v1=2m/s,同时释放木板B,并开动电动机保证A木块一直以v1沿斜面向下做匀速直线运动,直到木板B与挡板P接触时关闭电动机并锁定A、B位置.求:(1)B木板沿斜面向上加速运动过程的加速度大小;
(2)A、B沿斜面上升过程所经历的时间t;
(3)A、B沿斜面向下开始运动到木板B左端与P接触时,这段过程中A、B间摩擦产生的热量.
分析 (1)由牛顿第二定律可以求出B的加速度.
(2)由匀变速直线运动的速度公式求出B的速度等于A的速度需要的时间,然后由位移公式求出A、B的位移,然后应用匀速直线运动的位移公式求出A、B沿斜面上升过程的时间.
(3)由牛顿第二定律求B的加速度,应用运动学公式求出A、B的位移及A、B间的相对位移,然后求出因克服摩擦力产生的热量.
解答 解:(1)对B,由牛顿第二定律得:μ1Mgcosθ-mgsinθ=ma1,
代入数据解得:a1=2m/s2;
(2)A、B相对静止需要的时间为:t1=$\frac{{v}_{0}}{{a}_{1}}$=0.8s,
A的位移为:xA=v0t1=1.28m,
B的位移为:xB=$\frac{{v}_{0}}{2}$t1=0.64m,
AB的相对位移为:△x=xA-xB=0.64m,
A、B匀速运动的时间为:t=$\frac{L-d+△x}{{v}_{0}}$=1.15s;
(3)B开始向下加速运动的加速度为:a2=$\frac{{μ}_{2}Mgcosθ+mgsinθ}{m}$=10m/s2,
B与A相对静止后B的加速度为:a3=$\frac{mgsinθ-{μ}_{2}Mgcosθ}{m}$=2m/s2,
A、B相对静止的时间为:t2=$\frac{{v}_{1}}{{a}_{2}}$=0.2s,
A的位移为:xA′=v1t2=0.4m,
B的位移为:xB′=$\frac{{v}_{1}}{2}$t2=0.2m,
相对位移为:△x′=xA′-xB′=0.2m,
此时A离B右端的距离为:△x′+(d-△x)=0.36m,
AB速度相等后,B以加速度a2加速运动,B到达P所用时间为t3,
则:L-d-xB=v1t3+$\frac{1}{2}$a2t32,
代入数据解得:t3=($\sqrt{2}$-1)s,
A、B相对位移为:△x″=v1t3+$\frac{1}{2}$a2t32-v1t3=0.17m,
即:B与P接触时,A没有从B上滑离,
产生的热量为:Q=μ2Mgcosθ(△x′+△x″)=0.74J;
答:(1)B木板沿斜面向上加速运动过程的加速度大小为2m/s2;
(2)A、B沿斜面上升过程所经历的时间t为1.15s;
(3)A、B沿斜面向下开始运动到木板B左端与P接触时,这段过程中A、B间摩擦产生的热量为0.74J.
点评 本题考查了求加速度、物体的运动时间与产生的热量问题,本题是一道力学综合题,物体运动过程复杂,本题难度较大,分析清楚物体的运动过程是解题的关键,应用牛顿第二定律、运动学公式与功的计算公式可以解题.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案| A. | 为了有效地发射电磁波,应该采用长波发射 | |
| B. | 电磁波既有纵波,又有横波 | |
| C. | 均匀变化的电场产生均匀变化的磁场向外传播就形成了电磁波 | |
| D. | 根据相对论可知空间和时间与物质的运动状态有关 |
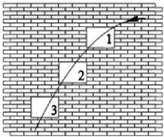 将一只苹果水平抛出,苹果在空中依次飞过三个完全相同的窗户1、2、3,图中曲线为苹果在空中运行的轨迹,不计空气阻力.下列说法正确的是( )
将一只苹果水平抛出,苹果在空中依次飞过三个完全相同的窗户1、2、3,图中曲线为苹果在空中运行的轨迹,不计空气阻力.下列说法正确的是( )| A. | 苹果通过第1个窗户所用的时间最长 | |
| B. | 苹果通过第3个窗户的过程中,竖直方向的平均速度最小 | |
| C. | 苹果通过第1个窗户的过程中,重力做功最多 | |
| D. | 苹果通过第2个窗户的过程中,重力的平均功率最大 |
| A. | 物体中分子热运动动能的总和等于物体的内能 | |
| B. | 橡胶无固定熔点,是非晶体 | |
| C. | 饱和汽压与分子密度有关,与温度无关 | |
| D. | 热机的效率总小于1 |
 用质量为M的吸铁石,将一张质量为m的白纸压在竖直固定的磁性黑板上.某同学沿着黑板面,用水平向右的恒力F轻拉吸铁石,吸铁石和白纸均未移动,如图所示.则下列说法中不正确的是( )
用质量为M的吸铁石,将一张质量为m的白纸压在竖直固定的磁性黑板上.某同学沿着黑板面,用水平向右的恒力F轻拉吸铁石,吸铁石和白纸均未移动,如图所示.则下列说法中不正确的是( )| A. | 吸铁石受到的摩擦力大小为Mg | |
| B. | 吸铁石受到的摩擦力大小为$\sqrt{{F}^{2}+(Mg)^{2}}$ | |
| C. | 白纸受到两个摩擦力的作用 | |
| D. | 白纸受到黑板的摩擦力大小为$\sqrt{{F}^{2}+(mg+Mg)^{2}}$ |
 如图所示,在两端封闭粗细均匀的竖直长管道内,用一可自由移动的活塞封闭体积相等的A、B两部分理想气体.开始时下部分B气体的压强pB=1.25×105Pa,活塞质量m=0.25kg,管内的横截面积S=1cm2,气体长度均为l0=9cm,现保持管道中气体温度不变,把管顺时针缓慢旋转至水平,不计活塞与管道壁间的摩擦,取g=10m/s2,求:管从竖直转到水平活塞移动的距离及管水平时气体的压强.
如图所示,在两端封闭粗细均匀的竖直长管道内,用一可自由移动的活塞封闭体积相等的A、B两部分理想气体.开始时下部分B气体的压强pB=1.25×105Pa,活塞质量m=0.25kg,管内的横截面积S=1cm2,气体长度均为l0=9cm,现保持管道中气体温度不变,把管顺时针缓慢旋转至水平,不计活塞与管道壁间的摩擦,取g=10m/s2,求:管从竖直转到水平活塞移动的距离及管水平时气体的压强. 在研究弹簧的伸长与外力的关系的实验中,将弹簧水平放置测出其自然长度,然后竖直悬挂让其自然下垂,在其下端竖直向下施加外力F,实验过程是在弹簧的弹性限度内进行的,用记录的外力F与弹簧的伸长量x作出的F-x图线如图所示.
在研究弹簧的伸长与外力的关系的实验中,将弹簧水平放置测出其自然长度,然后竖直悬挂让其自然下垂,在其下端竖直向下施加外力F,实验过程是在弹簧的弹性限度内进行的,用记录的外力F与弹簧的伸长量x作出的F-x图线如图所示.