题目内容
2. 如图所示,开口处有卡口、内截面积为S的导热性能良好的圆柱形气缸开口向上竖直放置在水平面上,缸内总体积为V0,大气压强为p0,一厚度不计、质量为m的活塞(m=0.2p0S/g)封住一定量的理想气体,温度为T0时缸内气体体积为0.8V0,先在活塞上缓慢放上质量为2m的砂子,然后逐渐升高缸内气体温度,求:
如图所示,开口处有卡口、内截面积为S的导热性能良好的圆柱形气缸开口向上竖直放置在水平面上,缸内总体积为V0,大气压强为p0,一厚度不计、质量为m的活塞(m=0.2p0S/g)封住一定量的理想气体,温度为T0时缸内气体体积为0.8V0,先在活塞上缓慢放上质量为2m的砂子,然后逐渐升高缸内气体温度,求:(1)初始时缸内气体的压强;
(2)活塞刚到达卡口处时,缸内气体的温度;
(3)当缸内气体的温度升高到2T0时,缸内气体的压强.
分析 (1)以活塞为研究对象,根据平衡列式求解;
(2)在活塞上放上质量为2m的砂子时缸内气体等温变化,根据玻意耳定律列式求解;
(3)缸内气体温度升高到2T0,气体先做等压变化后做等容变化,根据盖吕萨克定律和查理定律列式求解.
解答 解:(1)活塞静止,由平衡条件得p1s=p0s+mg
解得:P1=1.2p0
(2)在活塞上放上质量为2m的砂子时,以活塞为研究对象,由平衡得:
p2S=p0S+mg+2mg,
解得:p2=p0+$\frac{3mg}{s}$=1.6p0
等温过程,由p1V1=p2V2
解得V2=0.6V0
温度升高时气体先是等压过程,直到活塞上升到卡口为止,由盖吕萨克定律得
$\frac{{V}_{2}}{{T}_{0}}=\frac{{V}_{0}}{{T}_{1}}$
得T1=$\frac{5{T}_{0}}{3}$
(3)当缸内气体的温度升高到2T0过程,气体等容变化,由查理定律得:
$\frac{{P}_{2}}{{T}_{1}}=\frac{{P}_{3}}{{T}_{2}}$
代入数据解得:p3=1.92p0
答:(1)初始时缸内气体的压强为1.2P0;
(2)在活塞上放上质量为2m的砂子时缸内气体的体积为0.6V0;
(3)最后缸内气体的压强为1.92P0
点评 本题是气体的状态方程与静力学结合的问题,考查综合应用物理规律的能力.关键要明确气体的物理参数变化的情况,然后选择合适的气体实验定律列式求解.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
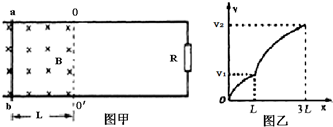
12. 如图所示,“U”形光滑金属框架宽度为L,与水平面夹角为θ,处于垂直导轨面向上的磁场中.一质量为m的金属棒ab从静止开始沿框架下滑,金属棒的运动速度v、所受安培力F随时间变化的图象正确的是( )
如图所示,“U”形光滑金属框架宽度为L,与水平面夹角为θ,处于垂直导轨面向上的磁场中.一质量为m的金属棒ab从静止开始沿框架下滑,金属棒的运动速度v、所受安培力F随时间变化的图象正确的是( )
 如图所示,“U”形光滑金属框架宽度为L,与水平面夹角为θ,处于垂直导轨面向上的磁场中.一质量为m的金属棒ab从静止开始沿框架下滑,金属棒的运动速度v、所受安培力F随时间变化的图象正确的是( )
如图所示,“U”形光滑金属框架宽度为L,与水平面夹角为θ,处于垂直导轨面向上的磁场中.一质量为m的金属棒ab从静止开始沿框架下滑,金属棒的运动速度v、所受安培力F随时间变化的图象正确的是( )| A. |  | B. |  | C. |  | D. |  |
13. 如图,水平地面上质量为m的物体,与地面的动摩擦因数为μ,在恒力F的作用下沿水平地面做加速度为a的匀加速直线运动,运动过程轻质弹簧没有超出弹性限度,则( )
如图,水平地面上质量为m的物体,与地面的动摩擦因数为μ,在恒力F的作用下沿水平地面做加速度为a的匀加速直线运动,运动过程轻质弹簧没有超出弹性限度,则( )
 如图,水平地面上质量为m的物体,与地面的动摩擦因数为μ,在恒力F的作用下沿水平地面做加速度为a的匀加速直线运动,运动过程轻质弹簧没有超出弹性限度,则( )
如图,水平地面上质量为m的物体,与地面的动摩擦因数为μ,在恒力F的作用下沿水平地面做加速度为a的匀加速直线运动,运动过程轻质弹簧没有超出弹性限度,则( )| A. | 物体受5个力作用 | B. | 弹簧的弹力为(μg+a)m | ||
| C. | 物体的加速度a=$\frac{F}{m}$ | D. | 弹簧的弹力小于物体所受合外力 |
10. 甲、乙两球位于同一竖直线上的不同位置,甲比乙高h,如图所示,将甲、乙两球分别以v1、v2的初速度沿同一方向抛出,不计空气阻力,下列条件中有可能使乙球击中甲球的是( )
甲、乙两球位于同一竖直线上的不同位置,甲比乙高h,如图所示,将甲、乙两球分别以v1、v2的初速度沿同一方向抛出,不计空气阻力,下列条件中有可能使乙球击中甲球的是( )
 甲、乙两球位于同一竖直线上的不同位置,甲比乙高h,如图所示,将甲、乙两球分别以v1、v2的初速度沿同一方向抛出,不计空气阻力,下列条件中有可能使乙球击中甲球的是( )
甲、乙两球位于同一竖直线上的不同位置,甲比乙高h,如图所示,将甲、乙两球分别以v1、v2的初速度沿同一方向抛出,不计空气阻力,下列条件中有可能使乙球击中甲球的是( )| A. | 甲比乙早抛出,且v1<v2 | B. | 甲比乙后抛出,且v1>v2 | ||
| C. | 甲比乙早抛出,且v1>v2 | D. | 同时抛出,且v1<v2 |
7. 质量为m的小球由轻绳a和b系于一轻质木架上的A点和C点,且La<Lb,如图所示.当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内作匀速圆周运动,绳a在竖直方向、绳b在水平方向.当小球运动在图示位置时,绳b被烧断的同时杆也停止转动,则( )
质量为m的小球由轻绳a和b系于一轻质木架上的A点和C点,且La<Lb,如图所示.当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内作匀速圆周运动,绳a在竖直方向、绳b在水平方向.当小球运动在图示位置时,绳b被烧断的同时杆也停止转动,则( )
 质量为m的小球由轻绳a和b系于一轻质木架上的A点和C点,且La<Lb,如图所示.当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内作匀速圆周运动,绳a在竖直方向、绳b在水平方向.当小球运动在图示位置时,绳b被烧断的同时杆也停止转动,则( )
质量为m的小球由轻绳a和b系于一轻质木架上的A点和C点,且La<Lb,如图所示.当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内作匀速圆周运动,绳a在竖直方向、绳b在水平方向.当小球运动在图示位置时,绳b被烧断的同时杆也停止转动,则( )| A. | 小球仍在水平面内作匀速圆周运动 | |
| B. | 在绳被烧断瞬间,a绳中张力不变 | |
| C. | 在绳被烧断瞬间,小球所受的合外力突然变小 | |
| D. | 若角速度ω较大,小球可以在竖直平面内作圆周运动 |
 如图所示,半径R=0.4m的圆盘水平放置,绕竖直轴OO′匀速转动,在圆心O正上方h=0.8m高处固定一水平轨道PQ,转轴和水平轨道交于O′点.一质量m=2kg的小车(可视为质点),在F=6N的水平恒力作用下(一段时间后,撤去该力),从O′左侧x0=2m处由静止开始沿轨道向右运动,当小车运动到O′点时,从小车上自由释放一小球,此时圆盘半径OA与x轴重合.规定经过O点水平向右为x轴正方向.小车与轨道间的动摩擦因数μ=0.2,g取10m/s2.
如图所示,半径R=0.4m的圆盘水平放置,绕竖直轴OO′匀速转动,在圆心O正上方h=0.8m高处固定一水平轨道PQ,转轴和水平轨道交于O′点.一质量m=2kg的小车(可视为质点),在F=6N的水平恒力作用下(一段时间后,撤去该力),从O′左侧x0=2m处由静止开始沿轨道向右运动,当小车运动到O′点时,从小车上自由释放一小球,此时圆盘半径OA与x轴重合.规定经过O点水平向右为x轴正方向.小车与轨道间的动摩擦因数μ=0.2,g取10m/s2. 竖直悬挂的弹簧振子下端装有记录笔,在竖直面内放置记录纸.当振子上下振动时,以水平向左速度v=10m/s匀速拉动记录纸,记录笔在纸上留下记录的痕迹,建立坐标系,测得的数据如图所示,则振子振动的振幅5cm,频率10Hz.
竖直悬挂的弹簧振子下端装有记录笔,在竖直面内放置记录纸.当振子上下振动时,以水平向左速度v=10m/s匀速拉动记录纸,记录笔在纸上留下记录的痕迹,建立坐标系,测得的数据如图所示,则振子振动的振幅5cm,频率10Hz.