题目内容
2.研究平抛物体的运动,在安装实验装置的过程中,斜槽末端的切线必须是水平的,这样做的目的是 ( )
| A. | 保证小球飞出时,速度既不太大,也不太小 | |
| B. | 保证小球飞出时,初速度水平 | |
| C. | 保证小球在空中运动的时间每次都相等 | |
| D. | 保证小球运动的轨道是一条抛物线 |
分析 在实验中让小球在固定斜槽滚下后,做平抛运动,记录下平抛后运动轨迹.然后在运动轨迹上标出特殊点,对此进行处理,由于是同一个轨迹,因此要求抛出的小球初速度是相同的,所以在实验时必须确保抛出速度方向是水平的,同时固定的斜槽要在竖直面.
解答 解:研究平抛运动的实验很关键的地方是要保证小球能够水平飞出,只有水平飞出时小球才做平抛运动,故ACD错误,B正确.
故选:B.
点评 在实验中如何实现让小球做平抛运动是关键,因此实验中关键是斜槽末端槽口的切线保持水平及固定后的斜槽要竖直.

练习册系列答案
相关题目
13.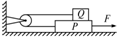 如图所示,物体Q重40N,物体P重80N,A与B、A与地面间的最大静摩擦力均为μ.滑轮的质量、滑轮轴上的摩擦都不计,若用一水平向右的力F=50N拉P使它做匀速运动,则μ大小为( )
如图所示,物体Q重40N,物体P重80N,A与B、A与地面间的最大静摩擦力均为μ.滑轮的质量、滑轮轴上的摩擦都不计,若用一水平向右的力F=50N拉P使它做匀速运动,则μ大小为( )
 如图所示,物体Q重40N,物体P重80N,A与B、A与地面间的最大静摩擦力均为μ.滑轮的质量、滑轮轴上的摩擦都不计,若用一水平向右的力F=50N拉P使它做匀速运动,则μ大小为( )
如图所示,物体Q重40N,物体P重80N,A与B、A与地面间的最大静摩擦力均为μ.滑轮的质量、滑轮轴上的摩擦都不计,若用一水平向右的力F=50N拉P使它做匀速运动,则μ大小为( )| A. | $\frac{1}{4}$ | B. | $\frac{5}{12}$ | C. | $\frac{5}{16}$ | D. | $\frac{1}{5}$ |
10.卫星甲绕质量为M1的行星以r1为半径做圆周运动,卫星乙绕质量为M2的行星以r2为半径做圆周运动,若不考虑某行星对另一行星的影响,用T1,T2和v1,v2分别表示卫星甲、乙的周期和线速度大小,则下列关系正确的是( )
| A. | $\frac{{{T}_{1}}^{2}}{{{T}_{2}}^{2}}$=$\frac{{{r}_{2}}^{3}}{{{r}_{1}}^{3}}$ | B. | $\frac{{{T}_{1}}^{2}}{{{T}_{2}}^{2}}$=$\frac{{M}_{2}{{r}_{1}}^{3}}{{M}_{1}{{r}_{2}}^{3}}$ | ||
| C. | $\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{{r}_{2}}{{r}_{1}}}$ | D. | $\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{{M}_{1{r}_{2}}}{{M}_{2}{r}_{1}}}$ |
17.关于物体做竖直上抛运动的说法,正确的是( )
| A. | 上升过程物体做减速运动,下落过程做加速运动 | |
| B. | 物体上升到最高点时速度为零,加速度为零 | |
| C. | 上升过程的加速度等于下落过程的加速度 | |
| D. | 物体以初速度v0抛出,落回抛出点时的速度与初速度相同,加速度也相同 |
7.匀速向东行驶的小车上有两球分别向东、向西同时水平抛出,抛出时两球的动量大小相等,则下列情况正确的是( )
| A. | 球抛出后,小车的速度不变 | B. | 球抛出后,小车的速度增大 | ||
| C. | 球抛出后,小车的速度减小 | D. | 向西抛出球的动量变化大 |
14.竖直上抛运动的物体,到达最高点时( )
| A. | 具有向上的速度和向下加速度 | B. | 速度为零,加速度向下 | ||
| C. | 速度为零,加速度向上 | D. | 具有向下的速度和向下加速度 |
11.用打点计时器研究物体运动时,接通电源和让纸带随物体开始运动,这两个操作的时间关系应当是( )
| A. | 先接通电源,后释放纸带 | B. | 先释放纸带,后接通电源 | ||
| C. | 先释放纸带或先接通电源都可以 | D. | 必须同时释放 |
4. 如图所示,ABC是半径为R的圆弧形光屏,ADC则是半径为R的圆弧形轨道,它们的圆心均为O,直线AOC是它们的直径.在光屏和轨道的中央安装半圆形玻璃砖,玻璃砖的平直面与直径AOC重合,在轨道ADC上安装光源P,从光源射出的光线沿着半圆形玻璃砖的半径射到它平直面上的中点O,在轨道上移动光源P可以改变入射光线PO与CO之间的夹角θ.现有两块尺寸相同,折射率不同的玻璃砖,在保持θ角相同时,分别安装甲、乙玻璃砖,折射光线分别射至光屏上M点和N点,则下列说法中正确的是( )
如图所示,ABC是半径为R的圆弧形光屏,ADC则是半径为R的圆弧形轨道,它们的圆心均为O,直线AOC是它们的直径.在光屏和轨道的中央安装半圆形玻璃砖,玻璃砖的平直面与直径AOC重合,在轨道ADC上安装光源P,从光源射出的光线沿着半圆形玻璃砖的半径射到它平直面上的中点O,在轨道上移动光源P可以改变入射光线PO与CO之间的夹角θ.现有两块尺寸相同,折射率不同的玻璃砖,在保持θ角相同时,分别安装甲、乙玻璃砖,折射光线分别射至光屏上M点和N点,则下列说法中正确的是( )
 如图所示,ABC是半径为R的圆弧形光屏,ADC则是半径为R的圆弧形轨道,它们的圆心均为O,直线AOC是它们的直径.在光屏和轨道的中央安装半圆形玻璃砖,玻璃砖的平直面与直径AOC重合,在轨道ADC上安装光源P,从光源射出的光线沿着半圆形玻璃砖的半径射到它平直面上的中点O,在轨道上移动光源P可以改变入射光线PO与CO之间的夹角θ.现有两块尺寸相同,折射率不同的玻璃砖,在保持θ角相同时,分别安装甲、乙玻璃砖,折射光线分别射至光屏上M点和N点,则下列说法中正确的是( )
如图所示,ABC是半径为R的圆弧形光屏,ADC则是半径为R的圆弧形轨道,它们的圆心均为O,直线AOC是它们的直径.在光屏和轨道的中央安装半圆形玻璃砖,玻璃砖的平直面与直径AOC重合,在轨道ADC上安装光源P,从光源射出的光线沿着半圆形玻璃砖的半径射到它平直面上的中点O,在轨道上移动光源P可以改变入射光线PO与CO之间的夹角θ.现有两块尺寸相同,折射率不同的玻璃砖,在保持θ角相同时,分别安装甲、乙玻璃砖,折射光线分别射至光屏上M点和N点,则下列说法中正确的是( )| A. | 甲玻璃砖的折射率小于乙玻璃砖的折射率 | |
| B. | 光在OM段的传播速度小于光在ON段的传播速度 | |
| C. | 光线沿P→O→M的传播时间大于光线沿P→O→N的传播时间 | |
| D. | 移动光源P逐渐增大θ角,则折射光线将会从光屏上消失 |
 如图所示,质量M=4kg、长L=3m的长木板放置于光滑的水平地面上,其左端有一大小可以忽略,质量为m=1kg的物块,物块和木板间的动摩擦因数为0.2.开始时物块和木板都处于静止状态,现在对物块施加F=4N,方向水平向右的恒定拉力,求:
如图所示,质量M=4kg、长L=3m的长木板放置于光滑的水平地面上,其左端有一大小可以忽略,质量为m=1kg的物块,物块和木板间的动摩擦因数为0.2.开始时物块和木板都处于静止状态,现在对物块施加F=4N,方向水平向右的恒定拉力,求: