题目内容
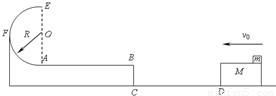
如图所示,水平路面CD的左侧有一固定的平台,平台上表面AB长s=3m.光滑半圆轨道AFE竖直固定在平台上,圆轨道半径 R=0.4m,最低点与平台AB相切于A.板长L1=2m,上表面与平台等高.小物块放在板的最右端,并随板一起向平台运动.当板的左端距离平台L=2m时,板与物块向左运动的速度v=8m/s.当板与平台的竖直墙壁碰撞后,板立即停止运动,物块在板上滑动,并滑上平台.已知板与路面的动摩擦因数µ1=0.05,物块与板的上表面及轨道AB的动摩擦因数µ2=0.1,物块质量m=1kg,取g=10m/s2.(1)求物块进入圆轨道时对轨道上A点的压力;
(2)判断物块能否到达圆轨道的最高点E.如果能,求物块离开E后在平台上的落点到A点的距离;如果不能,则说明理由.
【答案】分析:(1)由动能定理可求得滑块到达A点的速度,由牛顿第二定律即可求得压力;
(2)由临界条件可得出滑块能否到达最高点,若能到达则滑块做平抛运动,由平抛运动的位移规律可求得水平位移.
解答:解:(1)物块随车运动撞击平台时的速度v1满足:
-μ2(m+M)gL= (m+M)v12-
(m+M)v12- (M+m)v2
(M+m)v2
滑块到A点时速度v2满足:
-μ1mg(s+L1)= mv22-
mv22- mv12
mv12
由牛顿第二定律得:FN-mg=m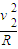
解得:FN=140N
由牛顿第三定律:滑块对轨道压力大小140N,方向竖直向下.
(2)设物块能通过圆轨道的最高点,且在最高点处的速度为v3,则有:
 mv22=
mv22= mv22+2mgR
mv22+2mgR
解得:v3=6m/s>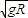 =2m/s
=2m/s
故能通过最高点,做平抛运动,有x=v3t
及2R= gt2
gt2
解得:x=2.4m
点评:本题要注意对过程的分析及研究对象的确定,明确了研究对象才能正确的应用动能定理及牛顿第二定律求解相应问题.
(2)由临界条件可得出滑块能否到达最高点,若能到达则滑块做平抛运动,由平抛运动的位移规律可求得水平位移.
解答:解:(1)物块随车运动撞击平台时的速度v1满足:
-μ2(m+M)gL=
 (m+M)v12-
(m+M)v12- (M+m)v2
(M+m)v2 滑块到A点时速度v2满足:
-μ1mg(s+L1)=
 mv22-
mv22- mv12
mv12 由牛顿第二定律得:FN-mg=m
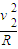
解得:FN=140N
由牛顿第三定律:滑块对轨道压力大小140N,方向竖直向下.
(2)设物块能通过圆轨道的最高点,且在最高点处的速度为v3,则有:
 mv22=
mv22= mv22+2mgR
mv22+2mgR 解得:v3=6m/s>
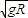 =2m/s
=2m/s 故能通过最高点,做平抛运动,有x=v3t
及2R=
 gt2
gt2 解得:x=2.4m
点评:本题要注意对过程的分析及研究对象的确定,明确了研究对象才能正确的应用动能定理及牛顿第二定律求解相应问题.

练习册系列答案
相关题目
 质量为lkg的物体在水平力作用下从静止开始做直线运动,物体沿水平路面运动的v-t关系如图所示,已知路面与物体间的动摩擦因数μ=0.2,则( )
质量为lkg的物体在水平力作用下从静止开始做直线运动,物体沿水平路面运动的v-t关系如图所示,已知路面与物体间的动摩擦因数μ=0.2,则( ) 如图所示,水平地面上停放着一辆实验小车,车与路面间的动摩擦因数为μ,车内左部固定的木柱高为h,其顶部静止着一个可视为质点的小球P,P与木柱接触光滑,现用一个水平向右的力拉小车,使小车由静止开始运动,实验过程中保持拉力的功率不变,经过时间t,小车达到最大速度,若在此时让小车瞬间停止运动,则小球水平向右抛出,最终落在车厢底板上,其水平位移为L.(已知重力加速度g,空气阻力不计).由以上信息,可求出的物理量是( )
如图所示,水平地面上停放着一辆实验小车,车与路面间的动摩擦因数为μ,车内左部固定的木柱高为h,其顶部静止着一个可视为质点的小球P,P与木柱接触光滑,现用一个水平向右的力拉小车,使小车由静止开始运动,实验过程中保持拉力的功率不变,经过时间t,小车达到最大速度,若在此时让小车瞬间停止运动,则小球水平向右抛出,最终落在车厢底板上,其水平位移为L.(已知重力加速度g,空气阻力不计).由以上信息,可求出的物理量是( )

