题目内容
1.1990年3月,紫金山天文台将1965年9月20日发现的第2752号小行星命名为吴健雄星,其半径R=16km,如该小行星的密度和地球的密度相同,则对该小行星而言,第一宇宙速度为多少(已知地球半径R0=6400km,地球的第一宇宙速度v1≈8km/s)?分析 因题目中是将吴健雄星与地球相比较,故应根据万有引力定律分别对地球和吴健雄星列出方程,通过作比得出小行星的第一宇宙速度.
解答 解:设小行星的第一宇宙速度为v2,其质量为M,地球质量为M0.则有
$\frac{GMm}{{R}^{2}}=m\frac{{{v}_{2}}^{2}}{R}$,
解得${v}_{2}=\sqrt{\frac{GM}{R}}$,
同理,地球的第一宇宙速度:${v}_{1}=\sqrt{\frac{G{M}_{0}}{{R}_{0}}}$,
又$M=ρ\frac{4}{3}π{R}^{3}$,
${M}_{0}=\frac{4}{3}π{{R}_{0}}^{3}$,
所以$\frac{{v}_{2}}{{v}_{1}}=\sqrt{\frac{M{R}_{0}}{{M}_{0}R}}$=$\frac{R}{{R}_{0}}$,
得${v}_{2}=\frac{R}{{R}_{0}}{v}_{1}=\frac{16×8×1{0}^{3}}{6400}m/s=20m/s$.
答:该小行星的第一宇宙速度为20 m/s
点评 本题要掌握第一宇宙速度的定义,正确利用万有引力公式列出第一宇宙速度的表达式.

练习册系列答案
相关题目
8. 如图所示是示波器原理图,电子被电压为U1的加速电场加速后射入电压为U2的偏转电场,离开偏转电场后电子打在荧光屏上的P点,P点与O点的距离叫做偏转距离,偏转电场极板长为L,板间距离为d,为了增大偏转距离,下列措施可行的是( )
如图所示是示波器原理图,电子被电压为U1的加速电场加速后射入电压为U2的偏转电场,离开偏转电场后电子打在荧光屏上的P点,P点与O点的距离叫做偏转距离,偏转电场极板长为L,板间距离为d,为了增大偏转距离,下列措施可行的是( )
 如图所示是示波器原理图,电子被电压为U1的加速电场加速后射入电压为U2的偏转电场,离开偏转电场后电子打在荧光屏上的P点,P点与O点的距离叫做偏转距离,偏转电场极板长为L,板间距离为d,为了增大偏转距离,下列措施可行的是( )
如图所示是示波器原理图,电子被电压为U1的加速电场加速后射入电压为U2的偏转电场,离开偏转电场后电子打在荧光屏上的P点,P点与O点的距离叫做偏转距离,偏转电场极板长为L,板间距离为d,为了增大偏转距离,下列措施可行的是( )| A. | 增大U1 | B. | 增大U2 | C. | 增大L | D. | 增大d |
12. 伽利略研究自由落体运动时,让小球从倾角较小的光滑斜面滑下,然后在不同的倾角条件下进行多次实验,实验示意图如图所示.则下列说法错误的是( )
伽利略研究自由落体运动时,让小球从倾角较小的光滑斜面滑下,然后在不同的倾角条件下进行多次实验,实验示意图如图所示.则下列说法错误的是( )
 伽利略研究自由落体运动时,让小球从倾角较小的光滑斜面滑下,然后在不同的倾角条件下进行多次实验,实验示意图如图所示.则下列说法错误的是( )
伽利略研究自由落体运动时,让小球从倾角较小的光滑斜面滑下,然后在不同的倾角条件下进行多次实验,实验示意图如图所示.则下列说法错误的是( )| A. | 斜面小角度是为了延长小球在斜面上运动的时间 | |
| B. | 实验结果说明小球在斜面上速度随时间均匀增加 | |
| C. | 实验结果说明小球在斜面上运动的距离随时间均匀增加 | |
| D. | 通过实验和逻辑推理,伽利略得出自由落体运动时一种匀加速直线运动 |
9.根据如图所示的振动图象,算出t1=0.5s时刻振子对平衡位置的位移,正确的是( )


| A. | 5$\sqrt{2}$ cm | B. | 5 cm | C. | -5$\sqrt{2}$ cm | D. | 6 cm |
13.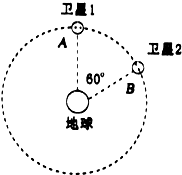 北京时间2015年3月30日2l时52分,我国新一代北斗导航卫星发射升空,卫星顺利进入预定轨道.“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均沿顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )
北京时间2015年3月30日2l时52分,我国新一代北斗导航卫星发射升空,卫星顺利进入预定轨道.“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均沿顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )
 北京时间2015年3月30日2l时52分,我国新一代北斗导航卫星发射升空,卫星顺利进入预定轨道.“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均沿顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )
北京时间2015年3月30日2l时52分,我国新一代北斗导航卫星发射升空,卫星顺利进入预定轨道.“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均沿顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )| A. | 这两颗卫星的加速度大小相等,均为$\frac{Rg}{r}$ | |
| B. | 这两颗卫星的线速度大小相等,均为$\sqrt{gr}$ | |
| C. | 卫星1向后喷气就一定能追上卫星2 | |
| D. | 卫星1由位置A运动到位置B所需的时间为$\frac{πr}{3Rg}$$\sqrt{gr}$ |
11.关于同步卫星下列说法正确的是( )
| A. | 若其质量加倍,则轨道半径也要加倍 | |
| B. | 它在北京上空运行,故可用于我国的电视广播 | |
| C. | 它以第一宇宙速度运行 | |
| D. | 它运行的角速度与地球自转角速度相同 |
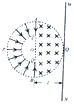 “太空粒子探测器”由加速、偏转和收集三部分装置组成,其原理如图所示:辐射状的加速电场区域边界为两个同心半圆弧$\widehat{AB}$和$\widehat{CD}$,圆心为O,弧$\widehat{AB}$的半径为L,P为弧$\widehat{AB}$的中点,两圆弧间的电势差大小为U.足够长的收集板MN平行于边界ACDB,0点到MN板的距离OQ为Lo在边界ACDB和收集板MN之间有一以0为圆心、L为半径的半圆形匀强磁场.方向垂直纸面向里.假设太空中漂浮着质量为m,电量为q的带正电粒子,它们能均匀地吸附到弧$\widehat{APB}$上,并被加速电场从静止开始加速,不汁粒子间的相互作用和其它星球对粒子引力的影响.
“太空粒子探测器”由加速、偏转和收集三部分装置组成,其原理如图所示:辐射状的加速电场区域边界为两个同心半圆弧$\widehat{AB}$和$\widehat{CD}$,圆心为O,弧$\widehat{AB}$的半径为L,P为弧$\widehat{AB}$的中点,两圆弧间的电势差大小为U.足够长的收集板MN平行于边界ACDB,0点到MN板的距离OQ为Lo在边界ACDB和收集板MN之间有一以0为圆心、L为半径的半圆形匀强磁场.方向垂直纸面向里.假设太空中漂浮着质量为m,电量为q的带正电粒子,它们能均匀地吸附到弧$\widehat{APB}$上,并被加速电场从静止开始加速,不汁粒子间的相互作用和其它星球对粒子引力的影响.