题目内容
17．图1所示为一列间谐横波在t=15秒时波形图，图2是这列波中P点的振动图线，那么该波的传播速度和传播方向是（ ）
| A． | v=50cm/s，向右传播 | B． | v=25cm/s，向左传播 | ||
| C． | v=50cm/s，向左传播 | D． | v=25cm/s，向右传播 |
分析 由甲图可读出波长，由乙图可读出周期，根据v=$\frac{λ}{T}$求出波速；图乙是质点P的振动图象，P点的振动是周期性的，则可读出t=15s时P的振动方向与1s时的振动方向相同，利用波形平移法判断波的传播方向．
解答 解：由两图象可知波长λ=100cm=1m，周期T=2s，则波速为 v=$\frac{λ}{T}$=$\frac{1}{2}$m/s=0.5m/s=50cm/s；
图乙是质点P的振动图象，P点的振动是周期性的，则可读出t=15s时P的振动方向与1s时的振动方向相同，由乙图可知t=15s时质点P向下振动，由波形平移可知波向右传播；故A正确，B、C、D错误．
故选：A．
点评 本题的关键理解和把握振动图象和波动图象的区别和联系，找出两种图象之间对应关系；波传播方向和质点的振动方向用波形平移法判断．
练习册系列答案
相关题目
7．物体万有引力场中具有的势能叫引力势能．取两物体相距无穷远时的引力势能为零．一个质量为m0的质点距离质量为M0的引力源中心为r0时，其引力势能EP=-$\frac{G{M}_{0}{m}_{0}}{{r}_{0}}$（式中G为引力常数）．一颗质量为m的人造地球卫星以圆形轨道环绕地球飞行，已知地球的质量为M，由于受高空稀薄空气的阻力作用．卫星的圆轨道半径从r1逐渐减小到r2，若在这个过程中空气阻力做功为Wf，则在下面给出的Wf的四个表达式中正确是（ ）
| A． | Wf=-GMm（$\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$） | B． | Wf=-$\frac{GMm}{2}$（$\frac{1}{{r}_{2}}$-$\frac{1}{{r}_{1}}$） | ||
| C． | Wf=-$\frac{GMm}{3}$（$\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$） | D． | Wf=-$\frac{2GMm}{3}$（$\frac{1}{{r}_{2}}$-$\frac{1}{{r}_{1}}$） |
5．在用如图示的实验装置做“碰撞中的动量守恒定律”实验中，下列说法正确的是（ ）
| A． | 斜糟轨道尽量光滑以减少误差 | |
| B． | 入射球和被碰球的质量必须相等，且大小相同 | |
| C． | 实验中不需要测量轨道末端离地面的高度 | |
| D． | 需要用圆规确定小球落地的平均位置，并用刻度尺测量落地水平距离 |
12．为了测量某行星的质量和半径，宇航员记录了登陆舱在该行星表面附近做圆周运动的周期为T，登陆舱在行星表面着陆后，用弹簧称量一个质量为m的砝码读数为N．已知引力常量为G．则下列计算中错误的是（ ）
| A． | 该行星的质量为$\frac{{N}^{3}{T}^{4}}{16G{π}^{4}{m}^{3}}$ | B． | 该行星的半径为$\frac{4{π}^{2}N{T}^{2}}{m}$ | ||
| C． | 该行星的密度为$\frac{3π}{G{T}^{2}}$ | D． | 该行星的第一宇宙速度为$\frac{NT}{2πm}$ |
如图所a示，水平地面上轻弹簧左端固定，右端通过滑块压缩0.4m锁定，t=0时解除锁定释放滑块．计算机通过滑块上的速度传感器描绘出滑块的速度图象如图b所示，其中Oab段为曲线，bc段为直线，倾斜直线Od是t=0s时的速度图线的切线，已知滑块质量m=10kg，取g=10m/s2，求：
9．下列电磁波中，频率最高的是（ ）
| A． | 无线电波 | B． | 红外线 | C． | 紫外线 | D． | γ射线 |
6．
如图甲所示，质量不计的弹簧竖直固定在水平地面上，t=0时刻，将一金属小球从弹簧正上方某一高度处由静止释放，小球落到弹簧上压缩弹簧到最低点，然后又被弹簧弹起离开弹簧，上升到一定高度后再下落，如此反复．通过安装在弹簧下端的压力传感器，测出这一过程弹簧弹力F随时间t变化的图象如图乙所示，则（ ）
如图甲所示，质量不计的弹簧竖直固定在水平地面上，t=0时刻，将一金属小球从弹簧正上方某一高度处由静止释放，小球落到弹簧上压缩弹簧到最低点，然后又被弹簧弹起离开弹簧，上升到一定高度后再下落，如此反复．通过安装在弹簧下端的压力传感器，测出这一过程弹簧弹力F随时间t变化的图象如图乙所示，则（ ）| A． | t2时刻弹簧的弹性势能最大 | |
| B． | t3时刻弹簧的弹性势能最大 | |
| C． | t1～t3这段时间内，弹簧的弹性势能先减小后增加 | |
| D． | t1～t3这段时间内，弹簧的弹性势能先增加后减少 |
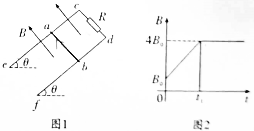如图1所示，由足够长的平行金属轨道ce、df确定的平面与水平面间的夹角为θ=60°，c、d端接有阻值为R的电阻，导体棒ab垂直于轨道放置在轨道上．轨道间距离为L，轨道间垂直于轨道平面向上的匀强磁场，磁感应强度B随时间t的变化规律如图2所示.0-t1时间内，棒ab静止在轨道上，且t1时刻恰好要沿轨道滑动，棒ab与cd端的距离为L．棒ab与两轨道接触良好，且其沿轨道下滑过程中始终与轨道垂直，轨道和棒的电阻不计，最大静摩擦力等于滑动摩擦力，求：