题目内容
A、B两行星绕同一恒星在同一平面内做匀速圆周运动,运行方向相同,A的轨道半径为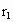 ,B的轨道半径为
,B的轨道半径为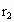 ,恒星质量为M,在某一时刻两行星相距最近.试求:(1)再经过多长时间两行星距离又最近?(2)再经过多长时间两行星距离最远?(已知恒星对行星的引力远大于行星间的引力,两行星的轨道半径
,恒星质量为M,在某一时刻两行星相距最近.试求:(1)再经过多长时间两行星距离又最近?(2)再经过多长时间两行星距离最远?(已知恒星对行星的引力远大于行星间的引力,两行星的轨道半径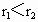 )
)
答案:略
解析:
解析:
|
(1) 如答图所示位置时距离最近,则A、B在同一条半径上.设A、B的角速度分别为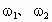 ,经过时间t,A转过的角度为 ,经过时间t,A转过的角度为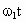 ,B转过的角度为 ,B转过的角度为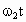 ,只有 ,只有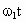 与 与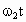 的差为2π整数倍时,A、B相距最近.所以 的差为2π整数倍时,A、B相距最近.所以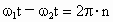 ,(n=1,2,3,…)而恒星对行星的万有引力提供向心力,所以 ,(n=1,2,3,…)而恒星对行星的万有引力提供向心力,所以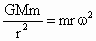 , ,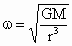 ,所以 ,所以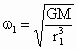 , ,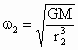 解得 解得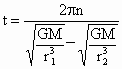 (n=1,2,3…) (n=1,2,3…)
(2) 若经过时间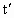 ,A、B转过的角度相差π的奇数倍时,A、B距离最远,则 ,A、B转过的角度相差π的奇数倍时,A、B距离最远,则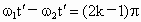 (k=1,2,3,…).所以 (k=1,2,3,…).所以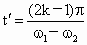 (k=1,2,3,…),将 (k=1,2,3,…),将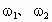 代入并整理得 代入并整理得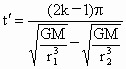 (k=1,2,3,…) (k=1,2,3,…)
|

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
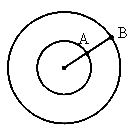
 如图所示,A和B两行星绕同一恒星C做圆周运动,旋转方向相同,A行星的周期为T1,B行星的周期为T2,某一时刻两行星相距最近,则( )
如图所示,A和B两行星绕同一恒星C做圆周运动,旋转方向相同,A行星的周期为T1,B行星的周期为T2,某一时刻两行星相距最近,则( )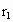 ,B的轨道半径为
,B的轨道半径为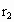 ,恒星质量为M,在某一时刻两行星相距最近.
,恒星质量为M,在某一时刻两行星相距最近.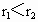 )
)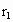 ,B的轨道半径为
,B的轨道半径为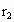 ,恒星质量为M,在某一时刻两行星相距最近.试求:(1)再经过多长时间两行星距离又最近?(2)再经过多长时间两行星距离最远?(已知恒星对行星的引力远大于行星间的引力,两行星的轨道半径
,恒星质量为M,在某一时刻两行星相距最近.试求:(1)再经过多长时间两行星距离又最近?(2)再经过多长时间两行星距离最远?(已知恒星对行星的引力远大于行星间的引力,两行星的轨道半径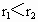 )
)