题目内容
5. 如图所示,为码头拖船作业的示意图,质量为m的汽车在平直路面上运动,用跨过光滑定滑轮的轻绳牵引轮船,汽车与定滑轮之间的轻绳始终水平.汽车加速行驶,当牵引轮船的轻绳与水平方向的夹角为θ时,汽车的加速度大小为a,牵引力的功率为P,受到的阻力大小为f,轮船的速度大小为v,则( )
如图所示,为码头拖船作业的示意图,质量为m的汽车在平直路面上运动,用跨过光滑定滑轮的轻绳牵引轮船,汽车与定滑轮之间的轻绳始终水平.汽车加速行驶,当牵引轮船的轻绳与水平方向的夹角为θ时,汽车的加速度大小为a,牵引力的功率为P,受到的阻力大小为f,轮船的速度大小为v,则( )| A. | 轮船在靠岸过程中可能做匀速运动 | |
| B. | 此时汽车的速度为v车=$\frac{v}{cosθ}$ | |
| C. | 此时绳的拉力T=$\frac{P}{vcosθ}$-ma-f | |
| D. | 此时绳的拉力对船做功的功率PT=P-(f+ma)vcosθ |
分析 对小船的速度分解,结合平行四边形定则得出车的速度,抓住车做匀速直线运动,得出船的运动规律.对汽车,运用牛顿第二定律求出绳子的拉力大小,结合瞬时功率公式求出拉力对船做功的功率.
解答 解:A、 由速度分解此时汽车的速度为:v车=v1=vcosθ,船靠岸的过程中,θ增大,cosθ减小,车的速度不变,则船速v增大,所以船做加速运动,故A错误,B错误.
由速度分解此时汽车的速度为:v车=v1=vcosθ,船靠岸的过程中,θ增大,cosθ减小,车的速度不变,则船速v增大,所以船做加速运动,故A错误,B错误.
C、对汽车,根据牛顿第二定律得,$\frac{P}{vcosθ}-f-T=ma$,解得此时拉力T=$\frac{P}{vcosθ}$-ma-f,故C正确.
D、此时绳子拉力对船做功的功率PT=Tvcosθ=P-(f+ma)vcosθ,故D正确.
故选:CD.
点评 解决本题的关键掌握功率与牵引力和速度的关系,注意船的速度和车的速度大小不等,船在沿绳子方向的分速度等于车的速度大小.

练习册系列答案
相关题目
13. 如图所示,质量相同的两个小物体A、B处于同一高度.现使A沿固定的光滑斜面无初速地自由下滑,而使B无初速地自由下落,最后A、B都运动到同一水平地面上.不计空气阻力.则在上述过程中,A、B两物体具有相同的( )
如图所示,质量相同的两个小物体A、B处于同一高度.现使A沿固定的光滑斜面无初速地自由下滑,而使B无初速地自由下落,最后A、B都运动到同一水平地面上.不计空气阻力.则在上述过程中,A、B两物体具有相同的( )
 如图所示,质量相同的两个小物体A、B处于同一高度.现使A沿固定的光滑斜面无初速地自由下滑,而使B无初速地自由下落,最后A、B都运动到同一水平地面上.不计空气阻力.则在上述过程中,A、B两物体具有相同的( )
如图所示,质量相同的两个小物体A、B处于同一高度.现使A沿固定的光滑斜面无初速地自由下滑,而使B无初速地自由下落,最后A、B都运动到同一水平地面上.不计空气阻力.则在上述过程中,A、B两物体具有相同的( )| A. | 重力的冲量 | B. | 合力的冲量 | ||
| C. | 刚到达底端时的动量 | D. | 刚到达底端时的动能 |
20.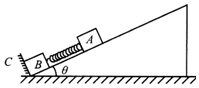 如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B.它们的质量均为m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现对物块A施加一沿斜面向下的瞬时冲量,使物块A在斜面上运动,当物块B刚要离开C时,物块A的速度为v,运动的位移大小为d.则在从施加冲量开始的整个过程中( )
如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B.它们的质量均为m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现对物块A施加一沿斜面向下的瞬时冲量,使物块A在斜面上运动,当物块B刚要离开C时,物块A的速度为v,运动的位移大小为d.则在从施加冲量开始的整个过程中( )
 如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B.它们的质量均为m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现对物块A施加一沿斜面向下的瞬时冲量,使物块A在斜面上运动,当物块B刚要离开C时,物块A的速度为v,运动的位移大小为d.则在从施加冲量开始的整个过程中( )
如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B.它们的质量均为m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现对物块A施加一沿斜面向下的瞬时冲量,使物块A在斜面上运动,当物块B刚要离开C时,物块A的速度为v,运动的位移大小为d.则在从施加冲量开始的整个过程中( )| A. | 弹簧对物块A做功为零 | |
| B. | A、B与弹簧组成的系统机械能守恒 | |
| C. | 物块A、B的质量满足2mgsinθ=kd | |
| D. | 弹簧的弹性势能的减小量为mdgsinθ+$\frac{1}{2}$mv2 |
17. 甲、乙、丙、丁是四个长度、横截面积均相同的金属导体,某同学对它们各进行了一次测量,把每个导体中通过的电流和两端的电压在I-U坐标系中描点,如图所示,四个导体中电阻率最大的是( )
甲、乙、丙、丁是四个长度、横截面积均相同的金属导体,某同学对它们各进行了一次测量,把每个导体中通过的电流和两端的电压在I-U坐标系中描点,如图所示,四个导体中电阻率最大的是( )
 甲、乙、丙、丁是四个长度、横截面积均相同的金属导体,某同学对它们各进行了一次测量,把每个导体中通过的电流和两端的电压在I-U坐标系中描点,如图所示,四个导体中电阻率最大的是( )
甲、乙、丙、丁是四个长度、横截面积均相同的金属导体,某同学对它们各进行了一次测量,把每个导体中通过的电流和两端的电压在I-U坐标系中描点,如图所示,四个导体中电阻率最大的是( )| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
14.如图所示,四个相同的小球A、B、C、D,其中A、B、C位于同一高度h处,A做自由落体运动,B沿光滑斜面由静止滑下,C做平抛运动,D从地面开始做斜抛运动,其运动的最大高度也为h.在每个小球落地的瞬间,其重力的功率分别为PA、PB、PC、PD.下列关系式正确的是( )


| A. | PA=PB=PC=PD | B. | PA=PC>PB=PD | C. | PA=PC=PD>PB | D. | PA>PC=PD>PB |
5. 如图所示,两根足够长的光滑平行金属导轨MN、PQ相距为L,导轨平面与水平面的夹角θ=30°,导轨电阻不计,整个装置处于磁感应强度大小为B、方向垂直导轨平面向上的匀强磁场中.质量为m、长为L、电阻为R的金属棒垂直导轨放置,且始终与导轨接触良好.金属导轨的上端连接一个阻值也为R的定值电阻.现闭合开关K,给金属棒施加一个平行于导轨斜向上、大小为F=2mg的恒力,使金属棒由静止开始运动.若金属棒上滑距离s时,金属棒开始匀速运动,则在金属棒由静止到刚开始匀速运动过程,下列说法中正确的是(重力加速度为g)( )
如图所示,两根足够长的光滑平行金属导轨MN、PQ相距为L,导轨平面与水平面的夹角θ=30°,导轨电阻不计,整个装置处于磁感应强度大小为B、方向垂直导轨平面向上的匀强磁场中.质量为m、长为L、电阻为R的金属棒垂直导轨放置,且始终与导轨接触良好.金属导轨的上端连接一个阻值也为R的定值电阻.现闭合开关K,给金属棒施加一个平行于导轨斜向上、大小为F=2mg的恒力,使金属棒由静止开始运动.若金属棒上滑距离s时,金属棒开始匀速运动,则在金属棒由静止到刚开始匀速运动过程,下列说法中正确的是(重力加速度为g)( )
 如图所示,两根足够长的光滑平行金属导轨MN、PQ相距为L,导轨平面与水平面的夹角θ=30°,导轨电阻不计,整个装置处于磁感应强度大小为B、方向垂直导轨平面向上的匀强磁场中.质量为m、长为L、电阻为R的金属棒垂直导轨放置,且始终与导轨接触良好.金属导轨的上端连接一个阻值也为R的定值电阻.现闭合开关K,给金属棒施加一个平行于导轨斜向上、大小为F=2mg的恒力,使金属棒由静止开始运动.若金属棒上滑距离s时,金属棒开始匀速运动,则在金属棒由静止到刚开始匀速运动过程,下列说法中正确的是(重力加速度为g)( )
如图所示,两根足够长的光滑平行金属导轨MN、PQ相距为L,导轨平面与水平面的夹角θ=30°,导轨电阻不计,整个装置处于磁感应强度大小为B、方向垂直导轨平面向上的匀强磁场中.质量为m、长为L、电阻为R的金属棒垂直导轨放置,且始终与导轨接触良好.金属导轨的上端连接一个阻值也为R的定值电阻.现闭合开关K,给金属棒施加一个平行于导轨斜向上、大小为F=2mg的恒力,使金属棒由静止开始运动.若金属棒上滑距离s时,金属棒开始匀速运动,则在金属棒由静止到刚开始匀速运动过程,下列说法中正确的是(重力加速度为g)( )| A. | 金属棒的末速度为$\frac{3mgR}{{{B^2}{L^2}}}$ | |
| B. | 金属棒的最大加速度为1.4g | |
| C. | 通过金属棒的电荷量为$\frac{BLs}{R}$ | |
| D. | 定值电阻上产生的焦耳热为$\frac{3}{4}$mgs-$\frac{{9{m^3}{g^2}{R^2}}}{{4{B^4}{L^4}}}$ |

 如图甲所示,四分之一光滑圆弧轨道与平台在B点处相切,圆弧半径R=l m,质量为1kg的物块置于A点,A、B间距离为2m,物块与平台间的动摩擦因数为μ=0.2.现用水平恒力F拉物块,使之由静止开始向右运动,到B点时撤去拉力,物块刚好能滑到轨道最高点.(g=10m/s2)
如图甲所示,四分之一光滑圆弧轨道与平台在B点处相切,圆弧半径R=l m,质量为1kg的物块置于A点,A、B间距离为2m,物块与平台间的动摩擦因数为μ=0.2.现用水平恒力F拉物块,使之由静止开始向右运动,到B点时撤去拉力,物块刚好能滑到轨道最高点.(g=10m/s2)