题目内容
6．
如图所示是倾角θ=45°的斜坡，在斜坡底端P点正上方Q点以速度v0水平向左抛出一个小球A，小球恰好能以垂直斜坡的速度落在斜坡上，运动时间为t1．小球B从同一点Q自由下落，下落至P点的时间为t2．不计空气阻力．求t1与t2的比值．
分析 小球做平抛运动时，根据平抛运动的规律求出竖直分位移和水平分位移之比，求出运动的时间，然后根据几何关系求解出的自由落体运动的位移并求出时间．
解答 
解：设小球A垂直落在斜面上时速度为v，平抛运动的水平位移x，竖直位移y；小球B自由落体运动下落高度为h
对小球A：将其末速度v按水平方向和竖直方向分解，如图所示．
v y=gt1
tanθ=$\frac{{v}_{y}}{{v}_{0}}$=1
x=v0t1
y=$\frac{1}{2}$gt12
$\frac{y}{x}$=2tanθ
即为：x=2y，
对小球B有：h=$\frac{1}{2}$gt22
且h=x+y
代入数据，联立以上各式，得运动时间t1与t2之比为1：$\sqrt{3}$．
答：t1与t2的比值为1：$\sqrt{3}$．
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，结合运动学公式和几何关系灵活求解．
练习册系列答案
相关题目
17．
在光滑的水平面上，有两个带异种电荷的小球A和B，它们在相互之间的静电力作用下绕两者连线上某一定点O做匀速圆周运动，如图所示．已知小球A的质量为mA，电荷量是qA，小球B的质量为mB，电荷量是qB，且mA＞mB，qB＞qA，A、B两球的距离为L，静电力常量为k．则下列判断正确的是（ ）
在光滑的水平面上，有两个带异种电荷的小球A和B，它们在相互之间的静电力作用下绕两者连线上某一定点O做匀速圆周运动，如图所示．已知小球A的质量为mA，电荷量是qA，小球B的质量为mB，电荷量是qB，且mA＞mB，qB＞qA，A、B两球的距离为L，静电力常量为k．则下列判断正确的是（ ）| A． | 小球A做圆周运动的半径rA=$\frac{{{q_B}L}}{{{q_A}+{q_B}}}$ | |
| B． | 小球B做圆周运动的半径rB=$\frac{{{m_A}L}}{{{m_A}+{m_B}}}$ | |
| C． | 小球A做圆周运动的周期TA=2π$\sqrt{\frac{{{m_A}{m_B}{L^3}}}{{k{q_A}{q_B}（{m_A}+{m_B}）}}}$ | |
| D． | 小球B做圆周运动的线速度vB=$\sqrt{\frac{{k{q_A}{q_B}{m_A}}}{{（{m_A}+{m_B}）{m_B}L}}}$ |
如图所示，在倾角为37°的光滑斜面上有一根长为0.4m，质量为3×10-2 kg的通电直导线，电流I=1A，方向垂直纸面向外，导线用平行于斜面的轻绳拴住不动，整个装置放在磁感应强度每秒增加0.2T，方向竖直向上的磁场中，设t=0时，B=0，则需要多长时间斜面对导线的支持力为零？（g取10m/s2）
1．
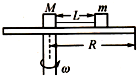如图所示，一圆盘可以绕其竖直轴在水平面内转动，圆盘半径为R，甲、乙两物体的质量分别为M和m（M＞m），两物体都可看做质点，它们与圆盘之间的最大静摩擦力均为正压力的μ倍，两物体用长为L的轻绳连在一起，L＜R．若将甲物体放在转轴位置上，甲、乙之间的连线正好沿半径方向拉直，从静止开始增大圆盘的转速，要使两物体与圆盘不发生相对滑动，圆盘旋转的角速度最大值ω1；若把甲、乙两物体一起向圆盘的边缘平移，使乙位于圆盘的边缘，甲、乙之间的连线仍然沿半径方向拉直，再次从静止开始增大圆盘的转速，要使两物体与圆盘不发生相对滑动，圆盘旋转的角速度最大值ω2．则ω1：ω2（ ）
如图所示，一圆盘可以绕其竖直轴在水平面内转动，圆盘半径为R，甲、乙两物体的质量分别为M和m（M＞m），两物体都可看做质点，它们与圆盘之间的最大静摩擦力均为正压力的μ倍，两物体用长为L的轻绳连在一起，L＜R．若将甲物体放在转轴位置上，甲、乙之间的连线正好沿半径方向拉直，从静止开始增大圆盘的转速，要使两物体与圆盘不发生相对滑动，圆盘旋转的角速度最大值ω1；若把甲、乙两物体一起向圆盘的边缘平移，使乙位于圆盘的边缘，甲、乙之间的连线仍然沿半径方向拉直，再次从静止开始增大圆盘的转速，要使两物体与圆盘不发生相对滑动，圆盘旋转的角速度最大值ω2．则ω1：ω2（ ）| A． | $\sqrt{\frac{mR+MR-ML}{mL}}$ | B． | $\sqrt{\frac{R}{L}}$ | C． | $\sqrt{\frac{2R-L}{L}}$ | D． | $\sqrt{\frac{M（R-L）}{mR}}$ |
11．
如图，倾角为30°的斜面体置于水平地面上，一根不可伸长的轻绳两端分别系着小球A和物块B，跨过固定于斜面体顶端的滑轮O（可视为质点）．A的质量为m，B的质量为4m，开始时，用手托住A，使OA段绳恰处于水平伸直状态（绳中无拉力），OB绳平行于斜面，此时B静止不动，将A由静止释放，在其下摆过程中斜面体始终保持静止，则在绳子到达竖直位置之前，下列说法正确的是（ ）
如图，倾角为30°的斜面体置于水平地面上，一根不可伸长的轻绳两端分别系着小球A和物块B，跨过固定于斜面体顶端的滑轮O（可视为质点）．A的质量为m，B的质量为4m，开始时，用手托住A，使OA段绳恰处于水平伸直状态（绳中无拉力），OB绳平行于斜面，此时B静止不动，将A由静止释放，在其下摆过程中斜面体始终保持静止，则在绳子到达竖直位置之前，下列说法正确的是（ ）| A． | 物块B与斜面之间的摩擦因数至少为$\frac{\sqrt{3}}{3}$ | |
| B． | 物块B受到的摩擦力先增大后减小 | |
| C． | 绳子的张力先减小后增大 | |
| D． | 地面对斜面体的摩擦力方向一直水平向左 |
15．洗衣机的甩干桶在工作匀速转动时有一衣物附在筒壁上，则此时（ ）
| A． | 筒壁对衣物的摩擦力随筒的转速的增大而增大 | |
| B． | 筒壁对衣服的弹力随筒的转速的增大而增大 | |
| C． | 衣服随筒壁做圆周运动的向心力是由所受的合力提供 | |
| D． | 衣服受到重力、筒壁的弹力、摩擦力 |
止释放，滑轮将在纸带带动下转动，假设纸带和滑轮不打滑，为了分析滑轮转动时角速度的变化情况，释放重物前将纸带先穿过一电火花打点计时器，如图b所示，通过测量纸带的运动情况得到滑轮角速度的变化情况．