题目内容
1.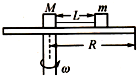 如图所示,一圆盘可以绕其竖直轴在水平面内转动,圆盘半径为R,甲、乙两物体的质量分别为M和m(M>m),两物体都可看做质点,它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用长为L的轻绳连在一起,L<R.若将甲物体放在转轴位置上,甲、乙之间的连线正好沿半径方向拉直,从静止开始增大圆盘的转速,要使两物体与圆盘不发生相对滑动,圆盘旋转的角速度最大值ω1;若把甲、乙两物体一起向圆盘的边缘平移,使乙位于圆盘的边缘,甲、乙之间的连线仍然沿半径方向拉直,再次从静止开始增大圆盘的转速,要使两物体与圆盘不发生相对滑动,圆盘旋转的角速度最大值ω2.则ω1:ω2( )
如图所示,一圆盘可以绕其竖直轴在水平面内转动,圆盘半径为R,甲、乙两物体的质量分别为M和m(M>m),两物体都可看做质点,它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用长为L的轻绳连在一起,L<R.若将甲物体放在转轴位置上,甲、乙之间的连线正好沿半径方向拉直,从静止开始增大圆盘的转速,要使两物体与圆盘不发生相对滑动,圆盘旋转的角速度最大值ω1;若把甲、乙两物体一起向圆盘的边缘平移,使乙位于圆盘的边缘,甲、乙之间的连线仍然沿半径方向拉直,再次从静止开始增大圆盘的转速,要使两物体与圆盘不发生相对滑动,圆盘旋转的角速度最大值ω2.则ω1:ω2( )| A. | $\sqrt{\frac{mR+MR-ML}{mL}}$ | B. | $\sqrt{\frac{R}{L}}$ | C. | $\sqrt{\frac{2R-L}{L}}$ | D. | $\sqrt{\frac{M(R-L)}{mR}}$ |
分析 当角速度从0开始增大,乙所受的静摩擦力开始增大,当乙达到最大静摩擦力,角速度继续增大,此时乙靠拉力和静摩擦力的合力提供向心力,角速度越大,拉力越大,当拉力和甲的最大静摩擦力相等时,角速度达到最大值,同理可以求出把甲、乙两物体一起向圆盘的边缘平移,使乙位于圆盘的边缘时的最大角速度,进而求出比值关系.
解答 解:当绳子的拉力等于甲的最大静摩擦力时,角速度达到最大,有:
T+μmg=mLω12,
T=μMg.
所以有:ω1=$\sqrt{\frac{μ(M+m)g}{mL}}$…①,
把甲、乙两物体一起向圆盘的边缘平移,当甲乙都达到最大静摩擦力时,圆盘转速最大,则有:
$μMg-T=M{{ω}_{2}}^{2}(R-L)$…②,
$μmg+T=m{{ω}_{2}}^{2}R$…③,
联立①②③解得:$\frac{{ω}_{1}}{{ω}_{2}}=\sqrt{\frac{mR+MR-ML}{mL}}$,故A正确.
故选:A
点评 解决本题的关键知道当角速度达到最大时,绳子的拉力等于甲的最大静摩擦力,乙靠拉力和乙所受的最大静摩擦力提供向心力

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11. 一个由绝缘轻绳和带电小球组成的单摆竖直悬挂,无外电场时,单摆摆线与竖直方向的夹角θ随时间t的变化图象如图,现施加一水平方向的匀强电场后,下列图象中不可能是该单摆的θ-t图象是( )
一个由绝缘轻绳和带电小球组成的单摆竖直悬挂,无外电场时,单摆摆线与竖直方向的夹角θ随时间t的变化图象如图,现施加一水平方向的匀强电场后,下列图象中不可能是该单摆的θ-t图象是( )
 一个由绝缘轻绳和带电小球组成的单摆竖直悬挂,无外电场时,单摆摆线与竖直方向的夹角θ随时间t的变化图象如图,现施加一水平方向的匀强电场后,下列图象中不可能是该单摆的θ-t图象是( )
一个由绝缘轻绳和带电小球组成的单摆竖直悬挂,无外电场时,单摆摆线与竖直方向的夹角θ随时间t的变化图象如图,现施加一水平方向的匀强电场后,下列图象中不可能是该单摆的θ-t图象是( )| A. |  | B. |  | C. |  | D. |  | ||||
| E. |  |
9.下列有关光的一些现象,说法错误的是( )
| A. | 日光照射在肥皂膜上出现彩色条纹是光的干涉现象 | |
| B. | 雨后出现彩虹是光的色散现象 | |
| C. | 白光通过三棱镜在屏上出现彩色条纹是光的干涉现象 | |
| D. | 汽车前挡风玻璃按同一要求设置,既防止对方强光刺眼,又方便看清前方路面,利用的是光的偏振 |
16.已知地球的第一宇宙速度为7.9km/s,第二宇宙速度为11.2km/s,下列叙述正确的是( )
| A. | 第一宇宙速度是物体在地面附近绕地球做匀速圆周运动的速度 | |
| B. | 第二宇宙速度是成为地球卫星的最小发射速度 | |
| C. | 所有地球卫星环绕地球的运行速度介于7.9km/s和11.2km/s之间 | |
| D. | 宇宙速度是相对于地面,而不是相对地心 |
13.在“蹦床”娱乐活动中,从小朋友下落到离地面高h1处开始计时,其动能EK与离地高度h的关系如图2所示.在h1一h2阶段图象为直线,其余部分为曲线,h3对应图象的最高点,小朋友的质量为m,重力加速度为g,不计空气阻力和一切摩擦.下列有关说法正确的是( )


| A. | 整个过程中小朋友的机械能守恒 | |
| B. | 从小朋友的脚接触蹦床直至蹦床被压缩至最低点的过程中,其加速度先减小后增大 | |
| C. | 小朋友处于h=h4高度时,蹦床的弹性势能为Ep=mg(h2-h4) | |
| D. | 小朋友从h1下降到h5过程中,蹦床的最大弹性势能为EPM=mgh1 |
10.小球从一个斜面的某一高度由静止滑下,并运动到另一个斜面的同一高度,小球好像“记得”自已的起始高度,或与高度相关的某个量.“记得”并不是物理学的语言.后来的物理学家把这一事实说成是“某个量是守恒的”,并且把这个量叫做( )
| A. | 重力 | B. | 势能 | C. | 能量 | D. | 速度 |
8. 如图所示,P、Q放置两个电量相等的异种电荷,它们连线的中点是O,N、a、b是中垂线上的三点,且oa=2ob,N处放置一负的点电荷,则( )
如图所示,P、Q放置两个电量相等的异种电荷,它们连线的中点是O,N、a、b是中垂线上的三点,且oa=2ob,N处放置一负的点电荷,则( )
 如图所示,P、Q放置两个电量相等的异种电荷,它们连线的中点是O,N、a、b是中垂线上的三点,且oa=2ob,N处放置一负的点电荷,则( )
如图所示,P、Q放置两个电量相等的异种电荷,它们连线的中点是O,N、a、b是中垂线上的三点,且oa=2ob,N处放置一负的点电荷,则( )| A. | a处的场强的大小小于b处的场强的大小 | |
| B. | a处的电势小于b处的电势 | |
| C. | a、O间的电势差大于a、b间的电势差2倍 | |
| D. | 电子在a处的电势能大于电子在b处的电势能 |
 在光滑绝缘的水平面上,沿x轴0到d范围内存在电场(图中未画出),电场的方向沿x轴正向,并且电场强度大小E随x的分布如图所示.将一质量为m1,电量为+q的小球A,从O点由静止释放.当小球A离开电场后与一个静止且不带电,质量为m2的小球B发生碰撞(设碰撞过程中无机械能损失、小球A、B大小相同,碰撞过程中电荷不发生转移).
在光滑绝缘的水平面上,沿x轴0到d范围内存在电场(图中未画出),电场的方向沿x轴正向,并且电场强度大小E随x的分布如图所示.将一质量为m1,电量为+q的小球A,从O点由静止释放.当小球A离开电场后与一个静止且不带电,质量为m2的小球B发生碰撞(设碰撞过程中无机械能损失、小球A、B大小相同,碰撞过程中电荷不发生转移). 如图所示是倾角θ=45°的斜坡,在斜坡底端P点正上方Q点以速度v0水平向左抛出一个小球A,小球恰好能以垂直斜坡的速度落在斜坡上,运动时间为t1.小球B从同一点Q自由下落,下落至P点的时间为t2.不计空气阻力.求t1与t2的比值.
如图所示是倾角θ=45°的斜坡,在斜坡底端P点正上方Q点以速度v0水平向左抛出一个小球A,小球恰好能以垂直斜坡的速度落在斜坡上,运动时间为t1.小球B从同一点Q自由下落,下落至P点的时间为t2.不计空气阻力.求t1与t2的比值.