题目内容
18.如图甲所示,xOy平面内虚线左侧存在着沿y轴正方向的匀强电场,虚线右侧有垂直纸面的磁场,磁感应强度B按如图乙所示的规律变化,设垂直纸面向外的磁场方向为正方向.某时刻一个带正电的粒子从坐标原点O以速度v0沿x轴正方向开始运动,在t=$\frac{T}{2}$时刻经过图中虚线上的P点进入磁场,t=$\frac{3T}{4}$时该粒子通过x轴且速度方向沿,y轴负方向,P点坐标为(2$\sqrt{3}$a,a),不计粒子的重力.试求:
(1)电场强度的大小.
(2)若P点坐标为(2$\sqrt{3}$,1),粒子速度v0=1×102m/s,求出粒子在磁场中运动的时间并做出粒子的运动过程轨迹示意图.
分析 (1)带电粒子从O到P做类平抛运动,根据牛顿第二定律和运动学规律结合可求得电场强度与初速度的关系式.粒子在磁场中做匀速圆周运动,画出轨迹,由几何关系求解轨迹半径,由牛顿第二定律得到半径与速度的关系式,联立可求得电场强度.
(2)粒子在磁场中做匀速圆周运动,结合轨迹的圆心角和周期,可求得时间.
解答  解:(1)设粒子的质量为m,电荷量为q,从O到P做类平抛运动,运动时间设为t,则有:
解:(1)设粒子的质量为m,电荷量为q,从O到P做类平抛运动,运动时间设为t,则有:
2$\sqrt{3}$a=v0t
a=$\frac{1}{2}•\frac{qE}{m}{t}^{2}$
得 E=$\frac{m{v}_{0}^{2}}{6qa}$
粒子运动到P点速度为v,与x方向的夹角为α,则有:
vy=$\frac{qE}{m}t$=$\frac{q}{m}$•$\frac{m{v}_{0}^{2}}{6qa}$•$\frac{2\sqrt{3}a}{{v}_{0}}$=$\frac{\sqrt{3}}{3}{v}_{0}$
v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\frac{2\sqrt{3}}{3}{v}_{0}$
tanα=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{\sqrt{3}}{3}$,
即:α=30°
粒子在磁场中做匀速圆周运动的轨迹半径为R,则有:R=$\frac{mv}{q{B}_{0}}$
画出轨迹,如图,由几何关系和题意可得:R=$\frac{2\sqrt{3}a}{3}$
由以上各式解得:E=$\frac{{B}_{0}{v}_{0}}{6}$
(2)粒子在磁场中做匀速圆周运动的周期:T1=$\frac{2πm}{q{B}_{0}}$=$\frac{2πa}{{v}_{0}}$
由几何关系可知粒子运动$\frac{T}{4}$轨迹对应的圆心角为 φ=120°
此过程粒子运动的时间为:t=$\frac{{T}_{1}}{3}$
根据磁感应强度B的变化规律,作出粒子的运动过程示意图.
由图可知粒子在磁场中运动的时间为:t′=$\frac{1}{3}{T}_{1}$+T1+$\frac{1}{3}{T}_{1}$=$\frac{5}{3}{T}_{1}$=$\frac{10πa}{3{v}_{0}}$
代入数据解得:t′=$\frac{10π}{3}×1{0}^{-2}$s
答:(1)电场强度的大小为$\frac{{B}_{0}{v}_{0}}{6}$.
(2)粒子在磁场中运动的时间为$\frac{10π}{3}×1{0}^{-2}$s,作出粒子的运动过程轨迹示意图如图.
点评 由该题看出,分清物理过程,不同物理过程应用相应的物理知识;抓住关键字句,分析出关键条件.在磁场中,利用相关知识来“定圆心,找半径”,画出轨迹,要有良好的作图能力及几何分析能力,这是解决此类问题的关键.

| A. | 若知道飞船运动的轨道半径和周期,再利用万有引力常量,就可以算出飞船质量 | |
| B. | “神舟八号”与“天宫一号”完成对接后,因质量变大,所受万有引力变大,飞船速率将变大 | |
| C. | 若有两个这样的飞船在同一圆轨道上,相隔一段距离一前一后沿同一方向绕行,只要后一飞船向后喷出气体,则两飞船一定能实现对接 | |
| D. | 若飞船执行完任务仅在地球万有引力作用下返回地球,在进入大气层之前的过程中,则飞船的动能逐渐增大,重力势能逐渐减小,机械能保持不变 |
 如图所示,实线是一簇未标明方向的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点.若带电粒子在运动中只受电场力的作用,对于a,b两点下列判断正确的是( )
如图所示,实线是一簇未标明方向的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点.若带电粒子在运动中只受电场力的作用,对于a,b两点下列判断正确的是( )| A. | 电场中a点的电势较高 | B. | 带电粒子在a点的动能较大 | ||
| C. | 带电粒子在a点的加速度较大 | D. | 带电粒子在a点的电势能较大 |
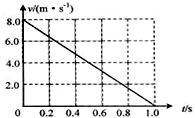 一质量m=2.0kg的小物块以一定的初速度冲上一倾角为37°足够长的斜面,某同学利用传感器测出了小物块冲上斜面过程中多个时刻的瞬时速度,并用计算机作出了小物块上滑过程的v-t图线,如图所示.(取sin 37°=0.6,cos 37°=0.8,g=10m/s2)求:
一质量m=2.0kg的小物块以一定的初速度冲上一倾角为37°足够长的斜面,某同学利用传感器测出了小物块冲上斜面过程中多个时刻的瞬时速度,并用计算机作出了小物块上滑过程的v-t图线,如图所示.(取sin 37°=0.6,cos 37°=0.8,g=10m/s2)求:
 如图所示,足够长光滑水平轨道与半径为R的光滑四分之一圆弧轨道相切.现从圆弧轨道的最高点由静止释放一质量为m的弹性小球A,当A球刚好运动到圆弧轨道的最低点时,与静止在该点的另一弹性小球B发生弹性碰撞.已知B球的质量是A球质量的k倍,且两球均可看成质点.
如图所示,足够长光滑水平轨道与半径为R的光滑四分之一圆弧轨道相切.现从圆弧轨道的最高点由静止释放一质量为m的弹性小球A,当A球刚好运动到圆弧轨道的最低点时,与静止在该点的另一弹性小球B发生弹性碰撞.已知B球的质量是A球质量的k倍,且两球均可看成质点. 在“用单摆测定重力加速度”的实验中:
在“用单摆测定重力加速度”的实验中: 如图所示为倾角为37°的斜面,一个质量1kg的滑块可以沿斜面匀速下滑,现将物块置于斜面的底端A点,用一水平向右的恒定推力F推动滑块,1s内滑块沿斜面上滑了1m,2s后撤去推力,滑块刚好能滑到斜面顶端,g=10m/s2,求:
如图所示为倾角为37°的斜面,一个质量1kg的滑块可以沿斜面匀速下滑,现将物块置于斜面的底端A点,用一水平向右的恒定推力F推动滑块,1s内滑块沿斜面上滑了1m,2s后撤去推力,滑块刚好能滑到斜面顶端,g=10m/s2,求: