题目内容
17.两颗人造地球卫星A和B的质量比mA:mB=1:2,轨道半径之比rA:rB=1:3,某一时刻它们的连线通过地心,则此时它们的线速度之比vA:vB=$\sqrt{3}$:1,向心加速度之比aA:aB=9:1.分析 该题考查万有引力定律及其应用,在该类的题目中,一定要使用万有引力提供向心力的公式解答.
解答 解:根据根据万有引力提供向心力,列出等式:
$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$=ma
v=$\sqrt{\frac{GM}{r}}$,轨道半径之比rA:rB=1:3,则此时它们的线速度之比vA:vB=$\sqrt{3}$:1,
T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,轨道半径之比rA:rB=1:3,则向心加速度之比aA:aB=9:1;
故答案为:$\sqrt{3}$:1;9:1
点评 该题考查万有引力定律及其应用,解题的关键在于一定要使用万有引力提供向心力的公式解答.属于基础题型,简单题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8. 经长期观测发现,A行星运行的轨道半径为R0,周期为T0,但其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.如图所示,天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则行星B运动轨道半径R( )
经长期观测发现,A行星运行的轨道半径为R0,周期为T0,但其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.如图所示,天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则行星B运动轨道半径R( )
 经长期观测发现,A行星运行的轨道半径为R0,周期为T0,但其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.如图所示,天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则行星B运动轨道半径R( )
经长期观测发现,A行星运行的轨道半径为R0,周期为T0,但其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.如图所示,天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则行星B运动轨道半径R( )| A. | R=R0$\root{3}{\frac{{{t}_{0}}^{2}}{({t}_{0}-{T}_{0})^{2}}}$ | B. | R=R0$\frac{{t}_{0}}{{t}_{0}-{T}_{0}}$ | ||
| C. | R=R0$\root{3}{\frac{({t}_{0}+{T}_{0})^{2}}{({t}_{0}-{T}_{0})^{2}}}$ | D. | R=R0$\root{3}{\frac{{t}_{0}}{{t}_{0}-{T}_{0}}}$ |
5. 如图所示,质量M=2kg、长L=2m的长木板静止放置在光滑水平面上,在其左端放置一质量m=1kg的小木块(可视为质点).先相对静止,然后用一水平向右、F=4N的力作用在小木块上,经过时间t=2s,小木块从长木板另一端滑出,取g=10m/s2,则( )
如图所示,质量M=2kg、长L=2m的长木板静止放置在光滑水平面上,在其左端放置一质量m=1kg的小木块(可视为质点).先相对静止,然后用一水平向右、F=4N的力作用在小木块上,经过时间t=2s,小木块从长木板另一端滑出,取g=10m/s2,则( )
 如图所示,质量M=2kg、长L=2m的长木板静止放置在光滑水平面上,在其左端放置一质量m=1kg的小木块(可视为质点).先相对静止,然后用一水平向右、F=4N的力作用在小木块上,经过时间t=2s,小木块从长木板另一端滑出,取g=10m/s2,则( )
如图所示,质量M=2kg、长L=2m的长木板静止放置在光滑水平面上,在其左端放置一质量m=1kg的小木块(可视为质点).先相对静止,然后用一水平向右、F=4N的力作用在小木块上,经过时间t=2s,小木块从长木板另一端滑出,取g=10m/s2,则( )| A. | 小木块与长木板之间的动摩擦因数为0.1 | |
| B. | 在整个运动过程中由于摩擦产生的热量为8J | |
| C. | 小木块脱离长木板的瞬间,拉力F的功率为16W | |
| D. | 长木板在运动过程中获得的机械能为16J |
9.下列说法正确的是( )
| A. | 公式E=$\frac{F}{q}$,只适用于真空中点电荷产生的电场 | |
| B. | 由公式E=$\frac{F}{q}$可知,电场中某点的电场强度与试探电荷在该点所受到的电场力成正比 | |
| C. | 在公式F=k$\frac{{Q}_{1}{Q}_{2}}{{r}^{2}}$中,k$\frac{{Q}_{2}}{{r}^{2}}$是点电荷Q2产生的电场在点电荷Q1处的场强大小 | |
| D. | 由公式F=k$\frac{{Q}_{1}{Q}_{2}}{{r}^{2}}$可知,在离场源电荷非常近的地方,电场强度可达无穷大 |
6. 某滑沙场有两个坡度不同的滑道AB和AB′(均可看作斜面),质量不相等的甲、乙两名旅游者分别乘两个完全相同的滑沙撬从A点由静止开始分别沿AB和AB′滑下,最后都停在水平沙面BC上,如图所示.设滑沙撬和沙面间的动摩擦因数处处相同,斜面与水平面连接处均可认为是圆滑的,滑沙者保持一定姿势坐在滑沙撬上不动.则下列说法中正确的是( )
某滑沙场有两个坡度不同的滑道AB和AB′(均可看作斜面),质量不相等的甲、乙两名旅游者分别乘两个完全相同的滑沙撬从A点由静止开始分别沿AB和AB′滑下,最后都停在水平沙面BC上,如图所示.设滑沙撬和沙面间的动摩擦因数处处相同,斜面与水平面连接处均可认为是圆滑的,滑沙者保持一定姿势坐在滑沙撬上不动.则下列说法中正确的是( )
 某滑沙场有两个坡度不同的滑道AB和AB′(均可看作斜面),质量不相等的甲、乙两名旅游者分别乘两个完全相同的滑沙撬从A点由静止开始分别沿AB和AB′滑下,最后都停在水平沙面BC上,如图所示.设滑沙撬和沙面间的动摩擦因数处处相同,斜面与水平面连接处均可认为是圆滑的,滑沙者保持一定姿势坐在滑沙撬上不动.则下列说法中正确的是( )
某滑沙场有两个坡度不同的滑道AB和AB′(均可看作斜面),质量不相等的甲、乙两名旅游者分别乘两个完全相同的滑沙撬从A点由静止开始分别沿AB和AB′滑下,最后都停在水平沙面BC上,如图所示.设滑沙撬和沙面间的动摩擦因数处处相同,斜面与水平面连接处均可认为是圆滑的,滑沙者保持一定姿势坐在滑沙撬上不动.则下列说法中正确的是( )| A. | 甲滑行的总路程一定大于乙滑行的总路程 | |
| B. | 甲在B点的动能一定大于乙在B′点的动能 | |
| C. | 甲在B点的速率一定大于乙在B′点的速率 | |
| D. | 甲全部滑行的水平位移一定大于乙全部滑行的水平位移 |
7.下列说法正确的是( )
| A. | 波的图象表示介质中“某个质点”在“各个时刻”的位移 | |
| B. | 当波源与观察者相互远离时,观察到的频率变小 | |
| C. | “空谷回音”是指声波的衍射现象 | |
| D. | 均匀变化的磁场产生均匀变化的电场,均匀变化的电场产生均匀变化的磁场 |
 要测量某电压表V1的内阻RV,其量程为2V,内阻约2kΩ.实验室提供的器材有:
要测量某电压表V1的内阻RV,其量程为2V,内阻约2kΩ.实验室提供的器材有: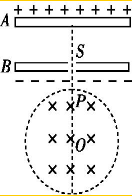 如图所示,一对带电平行金属板A、B水平放置,上下两极板间的电势差U=104V,两板间距d=10-2m,B板中央开有小孔S;金属板正下方有一半径R=10-2m的圆形的匀强磁场区域,磁场方向垂直于纸面向里,磁感应强度的大小B=1T,磁场区域的圆心O位于小孔正下方.SO连线交圆的边界于P点.比荷$\frac{q}{m}$=5×107C/kg的带正电粒子以速度v=5×105m/s从磁场外某处正对着圆心射向磁场区域,经过磁场的偏转作用,恰好沿着OP方向从小孔S进入电场.带电粒子在SP间运动的时间忽略不计,带电粒子的重力不计.求:
如图所示,一对带电平行金属板A、B水平放置,上下两极板间的电势差U=104V,两板间距d=10-2m,B板中央开有小孔S;金属板正下方有一半径R=10-2m的圆形的匀强磁场区域,磁场方向垂直于纸面向里,磁感应强度的大小B=1T,磁场区域的圆心O位于小孔正下方.SO连线交圆的边界于P点.比荷$\frac{q}{m}$=5×107C/kg的带正电粒子以速度v=5×105m/s从磁场外某处正对着圆心射向磁场区域,经过磁场的偏转作用,恰好沿着OP方向从小孔S进入电场.带电粒子在SP间运动的时间忽略不计,带电粒子的重力不计.求: