题目内容
5. 如图所示,固定于水平桌面上足够长的两平行导轨PQ、MN,PQ、MN的电阻不计,间距为d=0.5m.P、M两端接有一只理想电压表,整个装置处于竖直向下的磁感应强度B=0.2T的匀强磁场中.电阻分别为R1=0.4Ω、R2=0.1Ω、质量分别为m1=0.3kg和m2=0.5kg的两金属棒L1、L2平行的搁在光滑导轨上.现固定棒L1,L2在水平恒力F=0.4N的作用下,由静止开始做加速运动,求:
如图所示,固定于水平桌面上足够长的两平行导轨PQ、MN,PQ、MN的电阻不计,间距为d=0.5m.P、M两端接有一只理想电压表,整个装置处于竖直向下的磁感应强度B=0.2T的匀强磁场中.电阻分别为R1=0.4Ω、R2=0.1Ω、质量分别为m1=0.3kg和m2=0.5kg的两金属棒L1、L2平行的搁在光滑导轨上.现固定棒L1,L2在水平恒力F=0.4N的作用下,由静止开始做加速运动,求:(1)当电压表的读数为U=0.4V时,棒L2的速度v1和加速度a;
(2)棒L2能达到的最大速度vm的大小;
(3)若在棒L2达到最大速度vm时撤去外力F,并同时释放棒L1,求棒L2达到稳定时的速度值v;
(4)若固定棒L1,当棒L2的速度为v2,且离开棒L1距离为S的同时,撤去恒力F,为保持棒L2做匀速运动,可以采用将B从原值(B0=0.2T)逐渐减小的方法,则磁感应强度Bt应怎样随时间变化(写出Bt与时间t的关系式).
分析 (1)根据欧姆定律求解电流,求解出安培力,对右棒运用牛顿第二定律列式求解加速度;
(2)当安培力与拉力平衡时,速度达到最大;
(3)撤去恒力F后,两个棒系统受一对等大、反向的安培力,系统动量守恒,根据动量守恒定律列式求解即可;
(4)要使棒L2保持匀速运动,必须使回路中的磁通量保持不变,根据磁通量不变列式求解即可.
解答 解:(1)L1与L2串联,流过L1、L2的电流为:I=$\frac{U}{R_1}$=$\frac{0.4}{0.4}$=1A,
感应电动势:E=I(R1+R2)=1×(0.4+0.1)=0.5V,
感应电动势:E=Bdv1,解得:v1=$\frac{E}{Bd}$=$\frac{0.5}{0.2×0.5}$=5m/s,
L2所受安培力为:F安=BdI=0.2×0.5×1=0.1N,
由牛顿第二定律得,加速度:$a=\frac{{F-{F_安}}}{m_2}=\frac{0.4-0.1}{0.5}=0.6$m/s2;
(2)当L2所受安培力F安=F时,棒有最大速度vm,此时电路中电流为Im,
则:F安=BdIm,${I_m}=\frac{E_m}{{{R_1}+{R_2}}}$,Em=Bdvm,
由平衡条件得:F安=F,代入数据解得:vm=20m/s;
(3)撤去F后,棒L2做减速运动,L1做加速运动,当两棒达到共同速度v共时,
L2有稳定速度,此过程系统动量守恒,以向右为正方向,由动量守恒定律得:
m2vm=(m1+m2)v,代入数据解得:v=12.5 m/s;
(4)要使L2保持匀速运动,回路中磁通量必须保持不变,
设撤去恒力F时磁感应强度为B0,t时刻磁感应强度为Bt,
则:B0dS=Btd(S+v2t),解得:${B_t}=\frac{{{B_0}S}}{{S+{v_2}t}}$;
答:(1)当电压表的读数为U=0.4V时,棒L2的速度v1为5m/s,加速度a为0.6m/s2;
(2)棒L2能达到的最大速度vm的大小为20m/s;
(3)若在棒L2达到最大速度vm时撤去外力F,并同时释放棒L1,棒L2达到稳定时的速度值v为12.5m/s;
(4)磁感应强度Bt随时间变化的关系为:${B_t}=\frac{{{B_0}S}}{{S+{v_2}t}}$.
点评 本题关键明确:①撤去拉力后,两个棒系统动量守恒;②固定L1,要使棒L2保持匀速运动,必须使回路中的磁通量保持不变.

 如图所示,左侧的圆形导电环半径为r=2.0cm,导电环与一个理想变压器的原线圈相连,变压器的副线圈两端与一个电容为C=100μF的电容器相接,导电环的电阻不计,环中有垂直于圆环平面的变化磁场,磁场磁感应强度B的变化率$\frac{△B}{△t}$=100$\sqrt{2}$πsinωt,若电容器C所带电荷量的最大值为1.41×10-9C,则所用理想变压器的原副线圈的匝数之比是(取π2=10)( )
如图所示,左侧的圆形导电环半径为r=2.0cm,导电环与一个理想变压器的原线圈相连,变压器的副线圈两端与一个电容为C=100μF的电容器相接,导电环的电阻不计,环中有垂直于圆环平面的变化磁场,磁场磁感应强度B的变化率$\frac{△B}{△t}$=100$\sqrt{2}$πsinωt,若电容器C所带电荷量的最大值为1.41×10-9C,则所用理想变压器的原副线圈的匝数之比是(取π2=10)( )| A. | 25:1 | B. | 1:25 | C. | 141:4 | D. | 4:141 |
| A. | 如果用单色光1照射某种金属表面能够发射出光电子,那么用单色光2照射这种金属表面时也一定能够发射出光电子 | |
| B. | 如果用单色光2照射某种金属表面能够发射出光电子,那么用单色光1照射这种金属表面时也一定能够发射出光电子 | |
| C. | 如果用单色光1和2分别通过同一双缝干涉实验装置得到干涉条纹,则单色光1的相邻条纹间距小于单色光2的相邻条纹间距 | |
| D. | 在同一均匀介质中传播时,单色光1的传播速度大于单色光2的传播速度 |
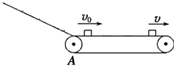 在工厂的流水线上安装有足够长的水平传送带,用水平传送带传送工件,可以大大提高工作效率,如图所示,水平传送带以恒定的速率v运送质量为m的工件,工件以v0(v0<v)的初速度从A位置滑上传送带,工件与传送带之间的动摩擦因数μ,已知重力加速度为g.( )
在工厂的流水线上安装有足够长的水平传送带,用水平传送带传送工件,可以大大提高工作效率,如图所示,水平传送带以恒定的速率v运送质量为m的工件,工件以v0(v0<v)的初速度从A位置滑上传送带,工件与传送带之间的动摩擦因数μ,已知重力加速度为g.( )| A. | 工件滑上传送带到与传送带相对静止所需时间为$\frac{v-{v}_{0}}{g}$ | |
| B. | 因传送工件电动机多做的功为$\frac{1}{2}$m(v2-v02) | |
| C. | 传送带的摩擦力对工件所做的功为$\frac{1}{2}$m(v-v0)2 | |
| D. | 工件与传送带的相对位移为$\frac{(v-{v}_{0})^{2}}{2μg}$ |
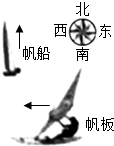
| A. | 帆船朝正东方向航行,速度大小为v | |
| B. | 帆船朝正西方向航行,速度大小为v | |
| C. | 帆船朝南偏东45°方向航行,速度大小为$\sqrt{2}$v | |
| D. | 帆船朝北偏东45°方向航行,速度大小为$\sqrt{2}$v |
 在倾斜角为θ的长斜面上,一带有风帆的滑块从静止开始沿斜面下滑,滑块(连同风帆)的质量为m,滑块与斜面间的动摩擦因数为μ,风帆受到的空气阻力与滑块下滑的速度v大小成正比,即f=kv(k未知),方向与v 的方向相反.滑块从静止开始沿斜面下滑的v-t图象如图所示,图中的倾斜直线是t=0时刻速度图线的切线.求:
在倾斜角为θ的长斜面上,一带有风帆的滑块从静止开始沿斜面下滑,滑块(连同风帆)的质量为m,滑块与斜面间的动摩擦因数为μ,风帆受到的空气阻力与滑块下滑的速度v大小成正比,即f=kv(k未知),方向与v 的方向相反.滑块从静止开始沿斜面下滑的v-t图象如图所示,图中的倾斜直线是t=0时刻速度图线的切线.求: 如图所示,质量为m小球,由长为l的细线系住,细线另一端固定在A点,AB是过A的竖直线,E为AB上的一点,且AE=0.5l,过E作水平线EF,在EF上钉铁钉D,已知线能承受的最大拉力是9mg.现将小球拉直水平,然后由静止释放,若小球能绕钉子在竖直面内做圆周运动,忽略空气阻力,不计线与钉子碰撞时的能量损失.
如图所示,质量为m小球,由长为l的细线系住,细线另一端固定在A点,AB是过A的竖直线,E为AB上的一点,且AE=0.5l,过E作水平线EF,在EF上钉铁钉D,已知线能承受的最大拉力是9mg.现将小球拉直水平,然后由静止释放,若小球能绕钉子在竖直面内做圆周运动,忽略空气阻力,不计线与钉子碰撞时的能量损失.