题目内容
8.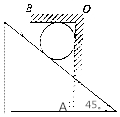 如图所示,倾角为45°直角三角形劈水平放置,质量为m的光滑圆球放在劈的斜面上,被固定在劈上的直角挡板AOB挡住,静止时,圆球顶部与水平挡板OB接触但无弹力.某时刻三角形劈在外力作用下先向左加速一段时间,然后改做加速度大小为a的减速运动,重力加速度为g,面说法正确的是( )
如图所示,倾角为45°直角三角形劈水平放置,质量为m的光滑圆球放在劈的斜面上,被固定在劈上的直角挡板AOB挡住,静止时,圆球顶部与水平挡板OB接触但无弹力.某时刻三角形劈在外力作用下先向左加速一段时间,然后改做加速度大小为a的减速运动,重力加速度为g,面说法正确的是( )| A. | 当球静止时,球对AO挡板的作用力FAO=$\sqrt{2}$mg | |
| B. | 减速阶段,当a=g时球对AO挡板的作用力FAO=mg | |
| C. | 减速阶段,当a>g时球对BO挡板的作用力FBO=m(a-g) | |
| D. | 减速阶段,当a<g时球对BO挡板的作用力FBO=m(g-a) |
分析 静止时,将重力进行分解,根据几何关系求解球对AO挡板的作用力;减速阶段,求出小球不受车厢的作用力加速度大小,然后根据牛顿第二定律分别讨论时a=g、a>g、a<g三种情况下球对板的作用力.
解答 解:A、静止时,将重力沿垂直斜面方向和垂直OA方向进行分解,根据几何关系可得球对AO挡板的作用力FAO=mg,故A错误;
B、减速阶段,设小球不受车厢的作用力,受力如图所示,
应满足:Nsinθ=ma,Ncosθ=mg,解得:a=gtan45°=g,所以当a=g时球对AO挡板的作用力FAO=0,故B错误;
C、减速阶段,当a>g时球对BO挡板的作用力,N′sinθ=ma,N′cosθ+FBO=mg,解得:FBO=m(a-g),故C正确;
D、减速阶段,当a<g时,球相对斜面有向下的运动趋势,所以OA对球产生作用力,球对BO挡板的作用力FBO=0,故D错误.
故选:C.
点评 本题主要是考查了牛顿第二定律的知识;利用牛顿第二定律答题时的一般步骤是:确定研究对象、进行受力分析、进行正交分解、在坐标轴上利用牛顿第二定律建立方程进行解答.

练习册系列答案
相关题目
13.1801年,一位英国科学家首次在实验室里观察到了光的干涉现象,他是( )
| A. | 托马斯•杨 | B. | 泊松 | C. | 牛顿 | D. | 麦克斯韦 |
11. 如图所示,一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间为0.01s.下列说法正确的是( )
如图所示,一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间为0.01s.下列说法正确的是( )
 如图所示,一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间为0.01s.下列说法正确的是( )
如图所示,一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间为0.01s.下列说法正确的是( )| A. | 球棒对垒球的平均作用力大小为360N | |
| B. | 球棒对垒球的平均作用力大小为1260N | |
| C. | 球棒对垒球做的功为36J | |
| D. | 球棒对垒球做的功为126J |
13. 如图所示,绝缘细杆倾斜固定放置,小球M套在杆上课沿杆滑动,M通过绝缘轻质弹簧与固定的小球N相连,杆和弹簧处于同一竖直面内,现使M、N带电荷量不同的异种电荷,将M从位置A由静止释放,M运动到B点时弹簧与杆垂直且为原长,运动到C点时速度减为零,M在A、C两点时弹簧长度相同,下列说法正确的是( )
如图所示,绝缘细杆倾斜固定放置,小球M套在杆上课沿杆滑动,M通过绝缘轻质弹簧与固定的小球N相连,杆和弹簧处于同一竖直面内,现使M、N带电荷量不同的异种电荷,将M从位置A由静止释放,M运动到B点时弹簧与杆垂直且为原长,运动到C点时速度减为零,M在A、C两点时弹簧长度相同,下列说法正确的是( )
 如图所示,绝缘细杆倾斜固定放置,小球M套在杆上课沿杆滑动,M通过绝缘轻质弹簧与固定的小球N相连,杆和弹簧处于同一竖直面内,现使M、N带电荷量不同的异种电荷,将M从位置A由静止释放,M运动到B点时弹簧与杆垂直且为原长,运动到C点时速度减为零,M在A、C两点时弹簧长度相同,下列说法正确的是( )
如图所示,绝缘细杆倾斜固定放置,小球M套在杆上课沿杆滑动,M通过绝缘轻质弹簧与固定的小球N相连,杆和弹簧处于同一竖直面内,现使M、N带电荷量不同的异种电荷,将M从位置A由静止释放,M运动到B点时弹簧与杆垂直且为原长,运动到C点时速度减为零,M在A、C两点时弹簧长度相同,下列说法正确的是( )| A. | M从A点滑到C点的过程,M和弹簧组成的系统的机械能守恒 | |
| B. | M从A点滑到C点的过程中,M的重力势能减少量等于其克服摩擦力做的功 | |
| C. | M从A点滑到B点的过程中,弹簧的弹力做正功,电场力做负功 | |
| D. | M在A、C两点的电势能相等 |
 如图所示,在方向竖直向上、大小为E=1×106V/m的匀强电场中,固定一个穿有A、B两个小球(均视为质点)的光滑绝缘圆环,圆环在竖直平面内,圆心为O、半径为R=0.2m.A、B用一根绝缘轻杆相连,A带的电荷量为q=+7×10-7C,B不带电,质量分别为mA=0.01kg、mB=0.08kg.将两小球从圆环上的图示位置(A与圆心O等高,B在圆心O的正下方)由静止释放,两小球开始沿逆时针方向转动.重力加速度大小为g=10m/s2.
如图所示,在方向竖直向上、大小为E=1×106V/m的匀强电场中,固定一个穿有A、B两个小球(均视为质点)的光滑绝缘圆环,圆环在竖直平面内,圆心为O、半径为R=0.2m.A、B用一根绝缘轻杆相连,A带的电荷量为q=+7×10-7C,B不带电,质量分别为mA=0.01kg、mB=0.08kg.将两小球从圆环上的图示位置(A与圆心O等高,B在圆心O的正下方)由静止释放,两小球开始沿逆时针方向转动.重力加速度大小为g=10m/s2.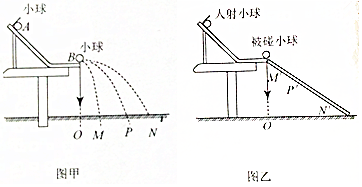
 如图所示,左侧的光滑斜面与右侧木板相连,把质量为m=l kg的滑块从斜面上高度h=0.1m处由静止释放,当右侧木板水平放置时,滑块在水平木板上滑行l=0.2m停止.欲使滑块从左侧斜面同一高度由静止下滑,并将右侧的木板向上转动一个锐角θ,形成斜面,使滑块在右侧木板上最远滑行0.l m,假设滑块由左侧斜面底端滑上右侧木板的瞬间速度大小不变.重力加速度g=10m/s2.求:θ的大小及滑块从冲上右侧木板到第一次返回最低点所用的时间.
如图所示,左侧的光滑斜面与右侧木板相连,把质量为m=l kg的滑块从斜面上高度h=0.1m处由静止释放,当右侧木板水平放置时,滑块在水平木板上滑行l=0.2m停止.欲使滑块从左侧斜面同一高度由静止下滑,并将右侧的木板向上转动一个锐角θ,形成斜面,使滑块在右侧木板上最远滑行0.l m,假设滑块由左侧斜面底端滑上右侧木板的瞬间速度大小不变.重力加速度g=10m/s2.求:θ的大小及滑块从冲上右侧木板到第一次返回最低点所用的时间.