题目内容
14.质量为1kg的物体从距地面1.8米高处落下,如果把整个过程看作是自由落体运动(g=10m/s2).求:(1)整个下落过程中所用的时间t
(2)整个下落过程中重力冲量I的大小
(3)物体落地前瞬间的动量P的大小.
分析 (1)由自由落体运动的公式即可求出运动的时间;
(2)由冲量的定义式即可求出重力的冲量;
(3)由动量定理即可求出动量.
解答 解:(1)整个下落过程中,由自由落体公式h=$\frac{1}{2}$gt2
代入数据得:t=0.6s
(2)整个下落过程中,重力的冲量I=mgt
代入数据得:I=6 N?s
(3)整个下落过程中,由动量定理mgt=mv-0
物体落地前瞬间的动量P=mv
代入数据得P=6kg?m/s
答:(1)整个下落过程中所用的时间是0.6s;
(2)整个下落过程中重力冲量I的大小是6Ns;
(3)物体落地前瞬间的动量P的大小是6kg?m/s.
点评 该题基于自由落体运动考查动量定理,解答的关键是要理解自由落体运动的过程中物体只受到重力的作用.
本题的第三问也可以由动量的定义求出.

练习册系列答案
相关题目
5. 如图所示,一辆小车装有光滑弧形轨道,总质量为m,停放在光滑水平面上.有一质量也为m的速度为v的铁球,沿轨道水平部分射入,并沿弧形轨道上升h后又下降而离开小车,离车后球的运动情况是( )
如图所示,一辆小车装有光滑弧形轨道,总质量为m,停放在光滑水平面上.有一质量也为m的速度为v的铁球,沿轨道水平部分射入,并沿弧形轨道上升h后又下降而离开小车,离车后球的运动情况是( )
 如图所示,一辆小车装有光滑弧形轨道,总质量为m,停放在光滑水平面上.有一质量也为m的速度为v的铁球,沿轨道水平部分射入,并沿弧形轨道上升h后又下降而离开小车,离车后球的运动情况是( )
如图所示,一辆小车装有光滑弧形轨道,总质量为m,停放在光滑水平面上.有一质量也为m的速度为v的铁球,沿轨道水平部分射入,并沿弧形轨道上升h后又下降而离开小车,离车后球的运动情况是( )| A. | 做自由落体运动 | |
| B. | 小球跟车有相同的速度 | |
| C. | 做平抛运动,速度方向跟车运动方向相反 | |
| D. | 做平抛运动,速度方向与车运动方向相同 |
2.半径相等的两个小球甲和乙,在光滑水平面上沿同一直线相向运动.若甲球的质量大于乙球的质量,碰撞前两球的动能相等,则碰撞后两球的运动状态,可能是( )
| A. | 甲球的速度为零而乙球的速度不为零 | |
| B. | 乙球的速度为零而甲球的速度不为零 | |
| C. | 两球的速度均不为零 | |
| D. | 两球的速度均与原方向相反,两球的动能仍相等 |
9.一辆小汽车,分别以相同的速率经过半径相同的拱形路面的最高点和凹形路面的最低点.车对拱形路面顶部的压力大小为N1,车对凹形路面底部的压力大小为N2,则N1与 N2的大小关系是( )


| A. | N1>N2 | B. | N1=N2 | C. | N1<N2 | D. | 无法判断 |
19. 如图所示,小明同学一分钟完成了 20个“引体向上”,若小明同学每次“引体向上”重心上升约0.5m,则在此过程中小明同学克服重力做功的平均功率接近( )
如图所示,小明同学一分钟完成了 20个“引体向上”,若小明同学每次“引体向上”重心上升约0.5m,则在此过程中小明同学克服重力做功的平均功率接近( )
 如图所示,小明同学一分钟完成了 20个“引体向上”,若小明同学每次“引体向上”重心上升约0.5m,则在此过程中小明同学克服重力做功的平均功率接近( )
如图所示,小明同学一分钟完成了 20个“引体向上”,若小明同学每次“引体向上”重心上升约0.5m,则在此过程中小明同学克服重力做功的平均功率接近( )| A. | 1000W | B. | 100W | C. | 10W | D. | 1W |
6.下列有关原子结构和原子核的认识,其中正确的是( )
| A. | 氢原子辐射光子后,其绕核运动的电子动能增大 | |
| B. | γ射线是高速运动的电子流 | |
| C. | 太阳辐射能量的主要来源是太阳中发生的重核裂变 | |
| D. | ${\;}_{83}^{210}Bi$的半衰期是5天,100克${\;}_{83}^{210}Bi$经过10天后还剩下50克 |
8.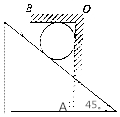 如图所示,倾角为45°直角三角形劈水平放置,质量为m的光滑圆球放在劈的斜面上,被固定在劈上的直角挡板AOB挡住,静止时,圆球顶部与水平挡板OB接触但无弹力.某时刻三角形劈在外力作用下先向左加速一段时间,然后改做加速度大小为a的减速运动,重力加速度为g,面说法正确的是( )
如图所示,倾角为45°直角三角形劈水平放置,质量为m的光滑圆球放在劈的斜面上,被固定在劈上的直角挡板AOB挡住,静止时,圆球顶部与水平挡板OB接触但无弹力.某时刻三角形劈在外力作用下先向左加速一段时间,然后改做加速度大小为a的减速运动,重力加速度为g,面说法正确的是( )
 如图所示,倾角为45°直角三角形劈水平放置,质量为m的光滑圆球放在劈的斜面上,被固定在劈上的直角挡板AOB挡住,静止时,圆球顶部与水平挡板OB接触但无弹力.某时刻三角形劈在外力作用下先向左加速一段时间,然后改做加速度大小为a的减速运动,重力加速度为g,面说法正确的是( )
如图所示,倾角为45°直角三角形劈水平放置,质量为m的光滑圆球放在劈的斜面上,被固定在劈上的直角挡板AOB挡住,静止时,圆球顶部与水平挡板OB接触但无弹力.某时刻三角形劈在外力作用下先向左加速一段时间,然后改做加速度大小为a的减速运动,重力加速度为g,面说法正确的是( )| A. | 当球静止时,球对AO挡板的作用力FAO=$\sqrt{2}$mg | |
| B. | 减速阶段,当a=g时球对AO挡板的作用力FAO=mg | |
| C. | 减速阶段,当a>g时球对BO挡板的作用力FBO=m(a-g) | |
| D. | 减速阶段,当a<g时球对BO挡板的作用力FBO=m(g-a) |
9.已知入射角i=60°,b光在三棱镜中的折射角r=45°,该三棱镜对b光的折射率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
 一根弹簧上端固定,下端系着质量为m的物体A,物A静止于O位置,如图所示.然后再用细线在A下挂一个物体B,重新平衡后将细线剪断,若A回到O点时的速度为v,此时B的速度为u,不计空气阻力,则这段时间内弹簧力对物体A的冲量的大小为mu+mv.
一根弹簧上端固定,下端系着质量为m的物体A,物A静止于O位置,如图所示.然后再用细线在A下挂一个物体B,重新平衡后将细线剪断,若A回到O点时的速度为v,此时B的速度为u,不计空气阻力,则这段时间内弹簧力对物体A的冲量的大小为mu+mv.