题目内容
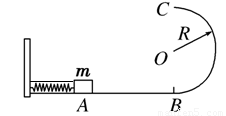
光滑水平面AB与竖直面的半圆形导轨在B点衔接,导轨半径R,如图所示,物块质量为m,弹簧处于压缩状态,现剪断细线,在弹力的作用下获得一个向右的速度,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动恰能完成半圆周运动到达C点,求:
(1)弹簧对物块的弹力做的功;
(2)物块从B至C克服摩擦阻力所做的功;
(3)物块离开C点后落回水平面时动能的大小
【答案】
(1)3mgR (2)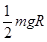 (3)
(3)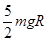
【解析】
试题分析:(1)设物块进入半圆导轨B点瞬间的速度为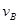 ,
,
物块到达B点时受重力mg和支持力N=7mg作用,
二者的合力提供向心力,则:
 ………………①
………………①
设弹簧对物块的弹力做的功为WF,对弹簧推动物块过程由动能定理得:
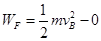 …………………②
…………………②
由①②解得:
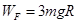 ……………………③
……………………③
(2)设物块到达C点时的速度为vC,依题意可知物块在C点仅受重力mg作用,对物块在C点由牛顿第二定律得:
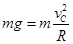 ………………………④
………………………④
设物块从B到C过程,摩擦阻力对物块所做功为Wf,对物块的此过程依动能定理得:
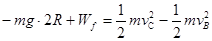 …⑤
…⑤
由①④⑤解得:
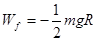 ……………………⑥
……………………⑥
故物块从B到C过程克服阻力做的功为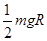 。
。
(3)设物块落回水平面AB时速度大小为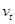 ,取水平面AB为重力势能零势面,对物块由C落到水平面AB的过程,依机械能守恒定律得:
,取水平面AB为重力势能零势面,对物块由C落到水平面AB的过程,依机械能守恒定律得:
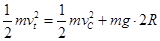 ………⑦
………⑦
由④⑦解得物块落回水平面AB时动能的大小为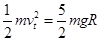 …………………⑧
…………………⑧
考点:机械能守恒定律的应用
点评:偏难。竖直平面内圆周运动,动能定理、机械能守恒是力学综合问题中经常用的物理规律,抓住每个规律的特点是解决这类问题的关键。

练习册系列答案
相关题目
 (2011?遵义县二模)如图,半径R=0.8m的四分之一光滑圆弧轨道位于竖直平面内,与长CD=2.0m的绝缘水平面平滑连接,水平面右侧空间存在互相垂直的匀强电场和匀强磁场,电场强度E=40
(2011?遵义县二模)如图,半径R=0.8m的四分之一光滑圆弧轨道位于竖直平面内,与长CD=2.0m的绝缘水平面平滑连接,水平面右侧空间存在互相垂直的匀强电场和匀强磁场,电场强度E=40 如图所示,光滑水平面AB与竖直平面内的光滑半圆导轨在B点相连接,导轨半径为R,一个质量为m的静止的木块在A处压缩弹簧,释放后,木块获得向右的初速度,当它经过B点进入半圆形导轨瞬间对导轨的压力是其重力的7倍,之后向上运动,C点为圆轨道最高点,试求:
如图所示,光滑水平面AB与竖直平面内的光滑半圆导轨在B点相连接,导轨半径为R,一个质量为m的静止的木块在A处压缩弹簧,释放后,木块获得向右的初速度,当它经过B点进入半圆形导轨瞬间对导轨的压力是其重力的7倍,之后向上运动,C点为圆轨道最高点,试求: 如图所示,水平面内的光滑轨道AB与竖直平面内的光滑弯曲轨道BC在B点相接.一小物块从AB上的D点以初速v0=4m/s出发向B点滑行,求:小物块能沿弯曲轨道上滑到距水平面的最大高度(设BC轨道足够长).
如图所示,水平面内的光滑轨道AB与竖直平面内的光滑弯曲轨道BC在B点相接.一小物块从AB上的D点以初速v0=4m/s出发向B点滑行,求:小物块能沿弯曲轨道上滑到距水平面的最大高度(设BC轨道足够长). (2011?台州模拟)如图所示,两条间距l=1m的光滑金属导轨制成的斜面和水平面,斜面的中间用阻值为R=2Ω的电阻连接.在水平导轨区域和斜面导轨及其右侧区域内分别有竖直向下和竖直向上的匀强磁场B1 和B2,且B1=B2=0.5T.在斜面的顶端e、f两点分别用等长轻质柔软细导线连接ab.ab和cd是质量均为m=0.1kg,长度均为1m的两根金属棒,ab棒电阻为r1=2Ω,cd棒电阻为r2=4Ω,cd棒置于水平导轨上且与导轨垂直,金属棒、导线及导轨接触良好.已知t=0时刻起,cd棒在外力作用下开始水平向右运动(cd棒始终在水平导轨上运动),ab棒受到F=0.75+0.2t(N)沿水平向右的力作用,始终处于静止状态且静止时细导线与竖直方向夹角θ=37°.导轨的电阻不计,图中的虚线为绝缘材料制成的固定支架.(g=10m/s2,sin37°=0.6,cos37°=0.8)
(2011?台州模拟)如图所示,两条间距l=1m的光滑金属导轨制成的斜面和水平面,斜面的中间用阻值为R=2Ω的电阻连接.在水平导轨区域和斜面导轨及其右侧区域内分别有竖直向下和竖直向上的匀强磁场B1 和B2,且B1=B2=0.5T.在斜面的顶端e、f两点分别用等长轻质柔软细导线连接ab.ab和cd是质量均为m=0.1kg,长度均为1m的两根金属棒,ab棒电阻为r1=2Ω,cd棒电阻为r2=4Ω,cd棒置于水平导轨上且与导轨垂直,金属棒、导线及导轨接触良好.已知t=0时刻起,cd棒在外力作用下开始水平向右运动(cd棒始终在水平导轨上运动),ab棒受到F=0.75+0.2t(N)沿水平向右的力作用,始终处于静止状态且静止时细导线与竖直方向夹角θ=37°.导轨的电阻不计,图中的虚线为绝缘材料制成的固定支架.(g=10m/s2,sin37°=0.6,cos37°=0.8)
