题目内容
10. 如图,一块质量为M=2kg,长L=1m的匀质木板放在足够长的光滑水平桌面上,初始时速度为零,板的最左端放置一个质量m=1kg的小物块,小物块与木板间的动摩擦因数为μ=0.2,小物块上连接一根足够长的水平轻质细绳,细绳跨过位于桌面边缘的定滑轮(细绳与滑轮间的摩擦不计,木板与滑轮之间距离足够长,g=10m/s2)
如图,一块质量为M=2kg,长L=1m的匀质木板放在足够长的光滑水平桌面上,初始时速度为零,板的最左端放置一个质量m=1kg的小物块,小物块与木板间的动摩擦因数为μ=0.2,小物块上连接一根足够长的水平轻质细绳,细绳跨过位于桌面边缘的定滑轮(细绳与滑轮间的摩擦不计,木板与滑轮之间距离足够长,g=10m/s2)(1)若木板被固定,某人以恒力F=4N向下拉绳,则小木块滑离木板所需要的时间是多少?
(2)若木板不固定,某人仍以恒力F=4N向下拉绳,则小木块滑离木板所需要的时间是多少?
分析 (1)若木板被固定,物块水平方向受到拉力和滑动摩擦力,根据牛顿第二定律求出物块的加速度,由运动学公式求解小木块滑离木板时的速度大小.
(2)若不固定木板,由牛顿第二定律分别对物块和木板研究,得到加速度,由位移公式分别列出两者的位移,根据两者位移之差等于板长L,联立求出时间,再由运动学公式求解速度.
解答 解:(1)对小物块受力分析,由牛顿第二定律得:F-μmg=ma
代入数据 可得:a=2m/s2
由运动学公式:v2=2aL
代入数据可得:v=2m/s
(2)对小物块、木板受力分析,由牛顿第二定律得:
F-μmg=ma1
μmg=Ma2,
代入解得a1=2m/s2,a2=1m/s2
物块的位移x1=$\frac{1}{2}{a}_{1}{t}^{2}$,木板的位移x2=$\frac{1}{2}{a}_{2}{t}^{2}$
又x1-x2=L
由以上三式可得t=$\sqrt{2}$s
可得v=a1t=2$\sqrt{2}$m/s
答:(1)若木板被固定,某人以恒力F=4N向下拉绳,则小木块滑离木板时的速度大小是2m/s;
(2)若不固定木板,某人仍以恒力F=4N向下拉绳,则小木块滑离木板时的速度大小是 2$\sqrt{2}$m/s.
点评 第(1)问也可以运用动能定理列方程求解:(F-μmg)L=$\frac{1}{2}m{v}^{2}$,解得v=2m/s.

练习册系列答案
相关题目
11. 温度能明显地影响金属导体和半导体材料的导电性能,在图所示的图象中分别为某金属和某半导体的电阻随温度变化的关系曲线,则( )
温度能明显地影响金属导体和半导体材料的导电性能,在图所示的图象中分别为某金属和某半导体的电阻随温度变化的关系曲线,则( )
 温度能明显地影响金属导体和半导体材料的导电性能,在图所示的图象中分别为某金属和某半导体的电阻随温度变化的关系曲线,则( )
温度能明显地影响金属导体和半导体材料的导电性能,在图所示的图象中分别为某金属和某半导体的电阻随温度变化的关系曲线,则( )| A. | 图线1反映半导体材料的电阻随温度的变化 | |
| B. | 图线2反映金属导体的电阻随温度的变化 | |
| C. | 图线1反映金属导体的电阻随温度的变化 | |
| D. | 图线2反映半导体材料的电阻随温度的变化 |
1. 如图所示在水平方向的匀强电场中,实线为电场线,方向未知,虚线为一带正电的粒子射入该电场后的运动轨迹,a,b是轨迹上先后的两点,根据以上可判断( )
如图所示在水平方向的匀强电场中,实线为电场线,方向未知,虚线为一带正电的粒子射入该电场后的运动轨迹,a,b是轨迹上先后的两点,根据以上可判断( )
 如图所示在水平方向的匀强电场中,实线为电场线,方向未知,虚线为一带正电的粒子射入该电场后的运动轨迹,a,b是轨迹上先后的两点,根据以上可判断( )
如图所示在水平方向的匀强电场中,实线为电场线,方向未知,虚线为一带正电的粒子射入该电场后的运动轨迹,a,b是轨迹上先后的两点,根据以上可判断( )| A. | 电场方向向右,a点电势较高 | B. | 电场方向向右,b点电势较高 | ||
| C. | 电场方向向左,a点电势较高 | D. | 电场方向向左,b点电势较高 |
18.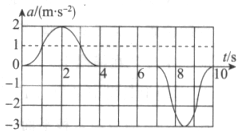 一同学在沿竖直方向运行的电梯中做实验,将重物置于放在电梯水平地板上的压力传感器的表面;将加速度传感器固定于电梯内.在电梯运行过程中加速度传感器的示数a随时间t变化的图线如图所示,以竖直向上方向为a的正方向,则以下判断正确的是( )
一同学在沿竖直方向运行的电梯中做实验,将重物置于放在电梯水平地板上的压力传感器的表面;将加速度传感器固定于电梯内.在电梯运行过程中加速度传感器的示数a随时间t变化的图线如图所示,以竖直向上方向为a的正方向,则以下判断正确的是( )
 一同学在沿竖直方向运行的电梯中做实验,将重物置于放在电梯水平地板上的压力传感器的表面;将加速度传感器固定于电梯内.在电梯运行过程中加速度传感器的示数a随时间t变化的图线如图所示,以竖直向上方向为a的正方向,则以下判断正确的是( )
一同学在沿竖直方向运行的电梯中做实验,将重物置于放在电梯水平地板上的压力传感器的表面;将加速度传感器固定于电梯内.在电梯运行过程中加速度传感器的示数a随时间t变化的图线如图所示,以竖直向上方向为a的正方向,则以下判断正确的是( )| A. | t=0到4 s的时间段内压力传感器的示数小于重物的重力值 | |
| B. | t=7 s到10 s的时间段内压力传感器的示数大于重物的重力值 | |
| C. | t=2 s时压力传感器的示数是重物重力值的2倍 | |
| D. | t=8.5 s时压力传感器的示数是重物重力值的0.7倍 |
20. 如图所示,水平传送带以v=2m/s的速度沿顺时针匀速转动,将一质量m=0.5kg的小物块(可视为质点)轻放在传送带最左端,在摩擦力的作用下,小物块会从传送带最右端水平飞出,恰好落在地面上某点P处,已知传送带左右两端相距l=3m,上端离地面高度h=5m,物块与传送带间的动摩擦因数μ=0.2,重力加速度g=10m/s2,则下列说法正确的是( )
如图所示,水平传送带以v=2m/s的速度沿顺时针匀速转动,将一质量m=0.5kg的小物块(可视为质点)轻放在传送带最左端,在摩擦力的作用下,小物块会从传送带最右端水平飞出,恰好落在地面上某点P处,已知传送带左右两端相距l=3m,上端离地面高度h=5m,物块与传送带间的动摩擦因数μ=0.2,重力加速度g=10m/s2,则下列说法正确的是( )
 如图所示,水平传送带以v=2m/s的速度沿顺时针匀速转动,将一质量m=0.5kg的小物块(可视为质点)轻放在传送带最左端,在摩擦力的作用下,小物块会从传送带最右端水平飞出,恰好落在地面上某点P处,已知传送带左右两端相距l=3m,上端离地面高度h=5m,物块与传送带间的动摩擦因数μ=0.2,重力加速度g=10m/s2,则下列说法正确的是( )
如图所示,水平传送带以v=2m/s的速度沿顺时针匀速转动,将一质量m=0.5kg的小物块(可视为质点)轻放在传送带最左端,在摩擦力的作用下,小物块会从传送带最右端水平飞出,恰好落在地面上某点P处,已知传送带左右两端相距l=3m,上端离地面高度h=5m,物块与传送带间的动摩擦因数μ=0.2,重力加速度g=10m/s2,则下列说法正确的是( )| A. | 小物块从轻放在传送带上到落到地面的时间为$\sqrt{3}$s | |
| B. | 落点P与传送带右端的水平距离为2$\sqrt{2}$m | |
| C. | 传送带因传送小物块多消耗的电能为2J | |
| D. | 小物块落到地面时的动能为26J |
 如图所示,质量m0=4kg的小车放在光滑的水平面上,在小车右端加一水平恒力F=6N,当小车向右运动的速度达到1.5m/s时,在小车前端轻轻放上一个大小不计、质量m=2kg的小物块,物块与小车间的动摩擦因数μ=0.2,物块始终没有离开小车,g取10m/s2,求:
如图所示,质量m0=4kg的小车放在光滑的水平面上,在小车右端加一水平恒力F=6N,当小车向右运动的速度达到1.5m/s时,在小车前端轻轻放上一个大小不计、质量m=2kg的小物块,物块与小车间的动摩擦因数μ=0.2,物块始终没有离开小车,g取10m/s2,求:
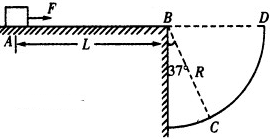 如图所示,水平地面的B点右侧有一圆形挡板,圆的半径R=4m,B为圆心,BC连线与竖直方向夹角为37°,滑块静止在水平地面上的A点,AB间距L=4.5m,现用水平拉力F=18N沿AB方向拉滑块,持续作用一段距离后撤去,滑块恰好落在圆形挡板的C点,已知滑块质量2kg,与水平地面间的动摩擦因数μ=0.4,取g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,水平地面的B点右侧有一圆形挡板,圆的半径R=4m,B为圆心,BC连线与竖直方向夹角为37°,滑块静止在水平地面上的A点,AB间距L=4.5m,现用水平拉力F=18N沿AB方向拉滑块,持续作用一段距离后撤去,滑块恰好落在圆形挡板的C点,已知滑块质量2kg,与水平地面间的动摩擦因数μ=0.4,取g=10m/s2,sin37°=0.6,cos37°=0.8,求: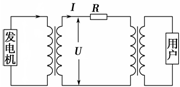 图为远距离输电的原理图,理想变压器原线圈输入功率为100KW,输电线上的电阻R为20Ω,采用10KV高压输电.则输电线路上损失的电压为200V,损失的电功率为2000W.
图为远距离输电的原理图,理想变压器原线圈输入功率为100KW,输电线上的电阻R为20Ω,采用10KV高压输电.则输电线路上损失的电压为200V,损失的电功率为2000W.