题目内容
15.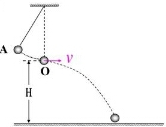 若小球摆到最低点时绳子断裂,小球水平飞出时的离地高度为H,则:
若小球摆到最低点时绳子断裂,小球水平飞出时的离地高度为H,则:(1)从飞出到落地的时间?
(2)小球落地时的速度多大?
(3)落地的速度方向?
分析 根据高度求出小球飞出到落地的时间,根据速度位移公式求出落地时竖直分速度,结合平行四边形定则求出小球落地的速度大小和方向.
解答 解:(1)根据H=$\frac{1}{2}g{t}^{2}$得:t=$\sqrt{\frac{2H}{g}}$.
(2)落地时竖直分速度为:${v}_{y}=\sqrt{2gH}$,
根据平行四边形定则知,落地的速度为:v′=$\sqrt{{v}^{2}+{{v}_{y}}^{2}}=\sqrt{{v}^{2}+2gH}$,
(3)设落地时速度方向与水平方向的夹角为α,则:$tanα=\frac{{v}_{y}}{v}=\frac{\sqrt{2gH}}{v}$.
答:(1)从飞出到落地的时间为$\sqrt{\frac{2H}{g}}$;
(2)小球落地的速度为$\sqrt{{v}^{2}+2gH}$;
(3)落地的速度方向与水平方向夹角的正切值为$\frac{\sqrt{2gH}}{v}$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,基础题.

练习册系列答案
相关题目
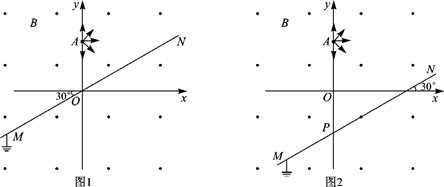
5. 如图所示,两光滑的平行导轨与水平方向成角同定,导轨的下端接有如图所示的电源,一劲度系数为k的轻质弹簧同定在导轨的顶端,下端拴接一导体棒ab,将整个装置置于垂直导轨平面向上的匀强磁场中.已知磁感应强度的大小为B,导轨的间距为L,当开关闭合后,导体棒ab平衡时,回路中的电流为I,弹簧的伸长量为x0.如果将电源反接,闭合开关后,导体棒ab再次平衡时,回路中的电流仍为I,电流产生的磁场可忽略不计,则弹簧的伸长量为( )
如图所示,两光滑的平行导轨与水平方向成角同定,导轨的下端接有如图所示的电源,一劲度系数为k的轻质弹簧同定在导轨的顶端,下端拴接一导体棒ab,将整个装置置于垂直导轨平面向上的匀强磁场中.已知磁感应强度的大小为B,导轨的间距为L,当开关闭合后,导体棒ab平衡时,回路中的电流为I,弹簧的伸长量为x0.如果将电源反接,闭合开关后,导体棒ab再次平衡时,回路中的电流仍为I,电流产生的磁场可忽略不计,则弹簧的伸长量为( )
 如图所示,两光滑的平行导轨与水平方向成角同定,导轨的下端接有如图所示的电源,一劲度系数为k的轻质弹簧同定在导轨的顶端,下端拴接一导体棒ab,将整个装置置于垂直导轨平面向上的匀强磁场中.已知磁感应强度的大小为B,导轨的间距为L,当开关闭合后,导体棒ab平衡时,回路中的电流为I,弹簧的伸长量为x0.如果将电源反接,闭合开关后,导体棒ab再次平衡时,回路中的电流仍为I,电流产生的磁场可忽略不计,则弹簧的伸长量为( )
如图所示,两光滑的平行导轨与水平方向成角同定,导轨的下端接有如图所示的电源,一劲度系数为k的轻质弹簧同定在导轨的顶端,下端拴接一导体棒ab,将整个装置置于垂直导轨平面向上的匀强磁场中.已知磁感应强度的大小为B,导轨的间距为L,当开关闭合后,导体棒ab平衡时,回路中的电流为I,弹簧的伸长量为x0.如果将电源反接,闭合开关后,导体棒ab再次平衡时,回路中的电流仍为I,电流产生的磁场可忽略不计,则弹簧的伸长量为( )| A. | $\frac{2BIL}{k}$+x0 | B. | $\frac{BIL}{k}$+x0 | C. | $\frac{2BIL}{k}$-x0 | D. | $\frac{BIL}{k}$-x0 |
6. 我国研制的“嫦娥三号”月球探测器于2013年12月1日发射成功,并成功在月球表面实现软着陆.卫星首先被送到距离月球表面高度为H的近月轨道做匀速圆周运动,之后再轨道上的A点实施变轨,使探测器绕月球做椭圆运动,当运动到B点时,继续变轨,使探测器靠近月球表面,当其距离月球表面高度为h(h<4m)时开始做自由落体运动,探测器携带的传感器测得自由落体运动时间为t,已知月球半径为R,万有引力常量为G,则下列说法正确的是( )
我国研制的“嫦娥三号”月球探测器于2013年12月1日发射成功,并成功在月球表面实现软着陆.卫星首先被送到距离月球表面高度为H的近月轨道做匀速圆周运动,之后再轨道上的A点实施变轨,使探测器绕月球做椭圆运动,当运动到B点时,继续变轨,使探测器靠近月球表面,当其距离月球表面高度为h(h<4m)时开始做自由落体运动,探测器携带的传感器测得自由落体运动时间为t,已知月球半径为R,万有引力常量为G,则下列说法正确的是( )
 我国研制的“嫦娥三号”月球探测器于2013年12月1日发射成功,并成功在月球表面实现软着陆.卫星首先被送到距离月球表面高度为H的近月轨道做匀速圆周运动,之后再轨道上的A点实施变轨,使探测器绕月球做椭圆运动,当运动到B点时,继续变轨,使探测器靠近月球表面,当其距离月球表面高度为h(h<4m)时开始做自由落体运动,探测器携带的传感器测得自由落体运动时间为t,已知月球半径为R,万有引力常量为G,则下列说法正确的是( )
我国研制的“嫦娥三号”月球探测器于2013年12月1日发射成功,并成功在月球表面实现软着陆.卫星首先被送到距离月球表面高度为H的近月轨道做匀速圆周运动,之后再轨道上的A点实施变轨,使探测器绕月球做椭圆运动,当运动到B点时,继续变轨,使探测器靠近月球表面,当其距离月球表面高度为h(h<4m)时开始做自由落体运动,探测器携带的传感器测得自由落体运动时间为t,已知月球半径为R,万有引力常量为G,则下列说法正确的是( )| A. | “嫦娥三号”的发射速度必须大于第一宇宙速度 | |
| B. | 探测器在近月圆轨道和椭圆轨道上的周期相等 | |
| C. | “嫦娥三号”在A点变轨时,需减速才能从近月圆规道进入椭圆轨道 | |
| D. | 月球的平均密度为$\frac{3h}{2πRG{t}^{2}}$ |
 飞行时间质谱仪可以根据带电粒子的飞行时间对气体分子进行分析.如图所示,在真空状态下,自脉冲阀P喷出微量气体,经激光照射产生不同正离子,自a板小孔进入a、b间的加速电场,从b板小孔射出,沿中线方向进入M、N板间的方形区域,然后到达紧靠在其右侧的探测器.已知极板a、b间的电压为U0,间距为d,极板M、N的长度和间距均为L.不计离子重力及经过a板时的初速度.
飞行时间质谱仪可以根据带电粒子的飞行时间对气体分子进行分析.如图所示,在真空状态下,自脉冲阀P喷出微量气体,经激光照射产生不同正离子,自a板小孔进入a、b间的加速电场,从b板小孔射出,沿中线方向进入M、N板间的方形区域,然后到达紧靠在其右侧的探测器.已知极板a、b间的电压为U0,间距为d,极板M、N的长度和间距均为L.不计离子重力及经过a板时的初速度.
 如图所示,A、B、C、D为匀强电场中相邻的四个等势面,并且AB=BC=CD,有一个电子垂直经过等势面D时动能为15eV,电子飞经等势面C时电势能为零,飞至等势面A时速度恰好为零,求:
如图所示,A、B、C、D为匀强电场中相邻的四个等势面,并且AB=BC=CD,有一个电子垂直经过等势面D时动能为15eV,电子飞经等势面C时电势能为零,飞至等势面A时速度恰好为零,求: 某同学根据所学知识设计了如图所示加速器,给质量为m,电量为+q的小球(视为质点)加速,两固定的平行金属板上下放置,板间固定一半径为R的竖直光滑绝缘圆轨道,在轨道最高点和最低点处各有一个感应器(视为质点).某时刻小球以初速度v0从轨道最低点水平向右冲入圆轨道,感应器立刻通过控制电路在两金属板间加上大小恒定的电压,使板间产生方向竖直向上的电场强度E,且qE=2mg,之后小球每经过一次感应器感应器就通过控制电路使电场反向一次:
某同学根据所学知识设计了如图所示加速器,给质量为m,电量为+q的小球(视为质点)加速,两固定的平行金属板上下放置,板间固定一半径为R的竖直光滑绝缘圆轨道,在轨道最高点和最低点处各有一个感应器(视为质点).某时刻小球以初速度v0从轨道最低点水平向右冲入圆轨道,感应器立刻通过控制电路在两金属板间加上大小恒定的电压,使板间产生方向竖直向上的电场强度E,且qE=2mg,之后小球每经过一次感应器感应器就通过控制电路使电场反向一次: