题目内容
6. 我国研制的“嫦娥三号”月球探测器于2013年12月1日发射成功,并成功在月球表面实现软着陆.卫星首先被送到距离月球表面高度为H的近月轨道做匀速圆周运动,之后再轨道上的A点实施变轨,使探测器绕月球做椭圆运动,当运动到B点时,继续变轨,使探测器靠近月球表面,当其距离月球表面高度为h(h<4m)时开始做自由落体运动,探测器携带的传感器测得自由落体运动时间为t,已知月球半径为R,万有引力常量为G,则下列说法正确的是( )
我国研制的“嫦娥三号”月球探测器于2013年12月1日发射成功,并成功在月球表面实现软着陆.卫星首先被送到距离月球表面高度为H的近月轨道做匀速圆周运动,之后再轨道上的A点实施变轨,使探测器绕月球做椭圆运动,当运动到B点时,继续变轨,使探测器靠近月球表面,当其距离月球表面高度为h(h<4m)时开始做自由落体运动,探测器携带的传感器测得自由落体运动时间为t,已知月球半径为R,万有引力常量为G,则下列说法正确的是( )| A. | “嫦娥三号”的发射速度必须大于第一宇宙速度 | |
| B. | 探测器在近月圆轨道和椭圆轨道上的周期相等 | |
| C. | “嫦娥三号”在A点变轨时,需减速才能从近月圆规道进入椭圆轨道 | |
| D. | 月球的平均密度为$\frac{3h}{2πRG{t}^{2}}$ |
分析 “嫦娥三号”在地表的发射速度大于第一宇宙速度小于第二宇宙速度;椭圆轨道的轨道半长轴和近月圆轨道的轨道半径不相等,因此周期不相同;从近月圆轨道需要点火减速做近心运动才能进入椭圆轨道;由月球表面物体的引力等于“重力”,得到月球质量M=$\frac{g{R}^{2}}{G}$,除以体积得到月球密度$ρ=\frac{3g}{4πGR}$,根据自由落体运动下落高度为h,运动时间为t,有h=$\frac{1}{2}g{t}^{2}$得到g=$\frac{2h}{{t}^{2}}$代入上述密度表达式中求出表达式即可判断正误
解答 解:A、“嫦娥三号”在地表的发射速度大于第一宇宙速度小于第二宇宙速度,故A正确;
B、椭圆轨道的轨道半长轴和近月圆轨道的轨道半径不相等,因此周期不相同,故B错误;
C、从近月圆轨道需要点火减速才能进入椭圆轨道,故C正确;
D、月球质量M=$\frac{g{R}^{2}}{G}$,除以体积得到月球密度$ρ=\frac{3g}{4πGR}$,根据自由落体运动下落高度为h,运动时间为t,有h=$\frac{1}{2}g{t}^{2}$得到g=$\frac{2h}{{t}^{2}}$代入上述密度表达式中,$ρ=\frac{3h}{2πGR{t}^{2}}$,故D正确.
故选:ACD
点评 运用黄金代换式GM=gR2求出问题是考试中常见的方法;要记住球体的体积公式;明白第一宇宙速度的意义;可以将椭圆运动近似堪为圆周运动,其半径为轨道半长轴

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
16.下列说法正确的是( )
| A. | 在美国,可以利用激光进行室内照明 | |
| B. | 用比值法定义的物理概念在物理学中占有相当大的比例,例如电场强度E=$\frac{F}{q}$,电容C=$\frac{Q}{U}$,加速度a=$\frac{F}{m}$都是采用比值法定义的 | |
| C. | 伽利略认为,自由落体运动就是物体在倾角为90°的斜面上运动,再根据铜球在斜面上的运动规律得出自由落体运动的运动规律,这采用了实验探究和逻辑推理向结合的方法 | |
| D. | 狭义相对论认为,在不同的惯性系中测量光在真空中的速率,其数值会不同 |
17.下列说法中正确的是( )
| A. | 两列波发生干涉时,振动加强的质点位移始终最大 | |
| B. | 无线网络信号能绕过障碍物传递到接收终端,这是利用了衍射原理 | |
| C. | 狭义相对性原理认为,在任何参考系中,物理规律都是相同的 | |
| D. | 观察者相对于频率一定的声源运动时,接收到声波的频率可能发生变化 | |
| E. | 变化电场的周围空间一定会产生磁场 |
14. 如图所示,竖直放置的弯曲管A端开口,B端封闭,密度为ρ的液体将两段空气封闭在管内.若大气压强为P0,管内液面高度为h1、h2、h3,则B端气体的压强为( )
如图所示,竖直放置的弯曲管A端开口,B端封闭,密度为ρ的液体将两段空气封闭在管内.若大气压强为P0,管内液面高度为h1、h2、h3,则B端气体的压强为( )
 如图所示,竖直放置的弯曲管A端开口,B端封闭,密度为ρ的液体将两段空气封闭在管内.若大气压强为P0,管内液面高度为h1、h2、h3,则B端气体的压强为( )
如图所示,竖直放置的弯曲管A端开口,B端封闭,密度为ρ的液体将两段空气封闭在管内.若大气压强为P0,管内液面高度为h1、h2、h3,则B端气体的压强为( )| A. | P0-ρg(h1+h2-h3) | B. | P0-ρg(h1+h3) | C. | P0-ρg(h1-h2+h3) | D. | P0-ρg(h1+h2) |
1. 在演示光电效应的实验中,把某种金同板连在验电器上.第一次,用弧光灯直接照射金属板,验电器的指针就张开一个角度.第二次,在弧光灯和金属板之间,插入一块普通的玻璃板,再用弧光灯照射,验电器指针不张开.由此可以判定,使金属板产生光电效应的是弧光中的( )
在演示光电效应的实验中,把某种金同板连在验电器上.第一次,用弧光灯直接照射金属板,验电器的指针就张开一个角度.第二次,在弧光灯和金属板之间,插入一块普通的玻璃板,再用弧光灯照射,验电器指针不张开.由此可以判定,使金属板产生光电效应的是弧光中的( )
 在演示光电效应的实验中,把某种金同板连在验电器上.第一次,用弧光灯直接照射金属板,验电器的指针就张开一个角度.第二次,在弧光灯和金属板之间,插入一块普通的玻璃板,再用弧光灯照射,验电器指针不张开.由此可以判定,使金属板产生光电效应的是弧光中的( )
在演示光电效应的实验中,把某种金同板连在验电器上.第一次,用弧光灯直接照射金属板,验电器的指针就张开一个角度.第二次,在弧光灯和金属板之间,插入一块普通的玻璃板,再用弧光灯照射,验电器指针不张开.由此可以判定,使金属板产生光电效应的是弧光中的( )| A. | 可见光成份 | B. | 紫外光成份 | C. | 红外光成份 | D. | 无线电波成份 |
18. 两个点电荷Q1、Q2固定于x轴上,将一带正电的试探电荷从足够远处沿x轴负方向移近Q2(位于坐标原点)的过程中,试探电荷的电势能Ep随位置变化的关系如图所示,则下列判断正确的是( )
两个点电荷Q1、Q2固定于x轴上,将一带正电的试探电荷从足够远处沿x轴负方向移近Q2(位于坐标原点)的过程中,试探电荷的电势能Ep随位置变化的关系如图所示,则下列判断正确的是( )
 两个点电荷Q1、Q2固定于x轴上,将一带正电的试探电荷从足够远处沿x轴负方向移近Q2(位于坐标原点)的过程中,试探电荷的电势能Ep随位置变化的关系如图所示,则下列判断正确的是( )
两个点电荷Q1、Q2固定于x轴上,将一带正电的试探电荷从足够远处沿x轴负方向移近Q2(位于坐标原点)的过程中,试探电荷的电势能Ep随位置变化的关系如图所示,则下列判断正确的是( )| A. | M点电势为零,N点场强为零 | |
| B. | M点场强为零,N点电势为零 | |
| C. | Q1带负电,Q2带正电,且Q2电荷量较大 | |
| D. | Q1带正电,Q2带负电,且Q2电荷量较大 |
16.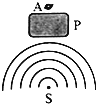 如图,P为桥墩,A为靠近桥墩浮在水面的叶片,波源S连续振动,形成水波,此时叶片A静止不动.为使水波能带动叶片振动,可用的方法是( )
如图,P为桥墩,A为靠近桥墩浮在水面的叶片,波源S连续振动,形成水波,此时叶片A静止不动.为使水波能带动叶片振动,可用的方法是( )
 如图,P为桥墩,A为靠近桥墩浮在水面的叶片,波源S连续振动,形成水波,此时叶片A静止不动.为使水波能带动叶片振动,可用的方法是( )
如图,P为桥墩,A为靠近桥墩浮在水面的叶片,波源S连续振动,形成水波,此时叶片A静止不动.为使水波能带动叶片振动,可用的方法是( )| A. | 提高波源频率 | B. | 降低波源频率 | ||
| C. | 增加波源距桥墩的距离 | D. | 减小波源距桥墩的距离 |
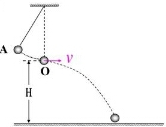 若小球摆到最低点时绳子断裂,小球水平飞出时的离地高度为H,则:
若小球摆到最低点时绳子断裂,小球水平飞出时的离地高度为H,则: