题目内容
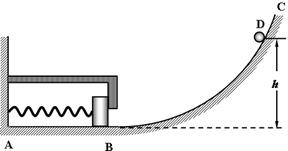
如图所示,ABC为光滑轨道,其中AB段水平,BC段是半径为R的圆弧,AB与BC相切于B点,A处有一竖直墙面,一轻弹簧的一端固定于墙上,另一端与一质量为M的物块相连接,当弹簧处于原长状态时,物块恰能与固定在墙上的L形挡板相接触于B处,但不挤压.现使一质量为m的小球从圆弧轨道上距水平轨道高h处的D点由静止下滑,小球与物块相碰后立即有相同速度但不粘连,此后物块与L形挡板相碰后速度立即减为0也不粘连.(整个过程,弹簧没有超过弹性限度,不计空气阻力,重力加速度为g
⑴试求弹簧获得的最大弹性势能;
⑵求小球与物块第一次碰后沿BC上升的最大高度;
⑶若R>>h,每次从小球接触物块至物块撞击L形挡板历时均为Δt,求小球由D点出发经多长时间第三次通过B点.
⑴ ![]()
⑵
![]()
⑶
![]()
解析:
⑴球从D下滑到B与物块碰前,小球机械能守恒,有![]() (2分)
(2分)
碰撞过程,小球与滑块系统动量守恒![]() (2分)
(2分)
碰后弹簧压缩到最大程度的过程中,M、m和弹簧的系统机械能守恒![]() (2分)
(2分)
解得![]() (2分
(2分
⑵第一次碰后,小球返回B点的速度仍为v1,设从B向C滑动的最大高度为h1,有
![]() (3分) 则
(3分) 则![]() (3分)
(3分)
⑶R>>h,小球在BC上的运动可等效为单摆,其周期为 ![]() (3分)
(3分)
分析知小球第三次通过B点经过的时间为 ![]() (3分)
(3分)

练习册系列答案
相关题目
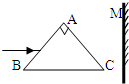 如图所示,ABC为一全反射棱镜,棱镜对不同色光折射不同,且对红光的临界角为42°,M为一与底边BC垂直的光屏,一束白光沿平行与底边BC的方向射向AB面,经AB面折射后的光线射向BC面,则( )
如图所示,ABC为一全反射棱镜,棱镜对不同色光折射不同,且对红光的临界角为42°,M为一与底边BC垂直的光屏,一束白光沿平行与底边BC的方向射向AB面,经AB面折射后的光线射向BC面,则( )| A、BC面将有色光射出 | B、光屏M上会出现色彩光带且紫光在上 | C、光屏M上会出现色彩光带且红光在上 | D、将光屏保持与BC垂直向右平移,屏上彩色光带宽度不变 |
 (2013?永州一模)如图所示,ABC为某种透明介质的横截面图,其中△AOC为等腰直角三角形,BC为半径R=10cm的四分之一圆弧,AB与水平屏幕MN垂直并接触于A点.由红光和紫光两种单色光组成的复色光经过BC面射向圆心O,在AB分界面上的入射角i=45°,结果在水平屏幕MN上出现两个亮斑,已知该介质对红光和紫光的折射率分别为n1=
(2013?永州一模)如图所示,ABC为某种透明介质的横截面图,其中△AOC为等腰直角三角形,BC为半径R=10cm的四分之一圆弧,AB与水平屏幕MN垂直并接触于A点.由红光和紫光两种单色光组成的复色光经过BC面射向圆心O,在AB分界面上的入射角i=45°,结果在水平屏幕MN上出现两个亮斑,已知该介质对红光和紫光的折射率分别为n1= 如图所示,△ABC为一直角三棱镜的截面,其顶角θ=30°,P为垂直于直线BCD的光屏.一束宽度等于AB的单色平行光束垂直射向AB面,经三棱镜折射后在屏P上形成一条光带.
如图所示,△ABC为一直角三棱镜的截面,其顶角θ=30°,P为垂直于直线BCD的光屏.一束宽度等于AB的单色平行光束垂直射向AB面,经三棱镜折射后在屏P上形成一条光带.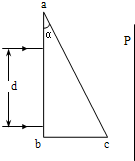 如图所示,△abc为一直角三棱镜的横截面,其顶角α=30°,P是平行于ab的光屏.现有一束宽度为d的单色平行光垂直射向ab面,结果在屏P上形成一宽度等于
如图所示,△abc为一直角三棱镜的横截面,其顶角α=30°,P是平行于ab的光屏.现有一束宽度为d的单色平行光垂直射向ab面,结果在屏P上形成一宽度等于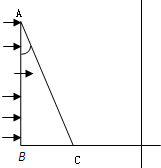 如图所示,△ABC为一直角三棱镜的截面,其顶角α=30°,BC边长为a,棱镜的折射率为
如图所示,△ABC为一直角三棱镜的截面,其顶角α=30°,BC边长为a,棱镜的折射率为