题目内容
7.${\;}_{1}^{3}$H的质量是3.016050u,质子的质量是1.007277u,中子的质量是1.008665u.(已知:原子质量单位1u=1.67×10-27kg,1u相当于931MeV)求:(1)一个质子和两个中子结合为氚核时,是吸收还是放出能量?该能量为多少?
(2)氚核的结合能和平均结合能各是多少?
(3)如果这些能量是以光子的形式放出,则光子的频率是多少?
分析 (1)根据电荷数守恒、质量数守恒写出核反应方程,结合爱因斯坦质能方程求出释放的能量;
(2)根据结合能与平均结合能的定义即可求出平均结合能;
(3)光子的能量为:E=hγ,根据公式即可求出光子的频率.
解答 解:(1)根据电荷数守恒、质量数守恒,一个质子和两个中子结合为氚核时得:
${\;}_{1}^{1}H$+2${\;}_{0}^{1}n$→${\;}_{1}^{3}H$
2个中子和1个质子结合成${\;}_{1}^{3}$H时质量亏损:△m=2mn+mP-mH=1.007277u+2×1.008665u-3.016050u=0.008557u,所以将放出能量;
根据爱因斯坦质能方程,放出的能量为:△E=△mc2=(2mn+mP-mHe)c2=0.008557×931.5=7.97MeV
(2)2个中子和1个质子结合成${\;}_{1}^{3}$H时放出的能量为7.97MeV,所以其结合能为7.97MeV
${\;}_{1}^{3}$H的平均结合能为:$\frac{△E}{3}=\frac{7.97}{3}=2.66$MeV
(3)光子的能量为:E=hγ
所以:$γ=\frac{△E}{h}=\frac{7.97×1{0}^{6}×1.6×1{0}^{-19}}{6.63×1{0}^{-34}}$=1.92×1021Hz
答:(1)一个质子和两个中子结合为氚核时,放出能量,该能量为7.97MeV;
(2)氚核的结合能和平均结合能各是7.97MeV,和2.66MeV;
(3)如果这些能量是以光子的形式放出,则光子的频率是1.92×1021Hz.
点评 本题考查了核反应方程和爱因斯坦质能方程的基本运用,比较简单,知道在核反应方程中电荷数守恒、质量数守恒.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
18.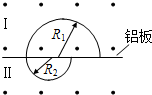 薄铝板将同一匀强磁场分成Ⅰ、Ⅱ两个区域,高速带电粒子可穿过铝板一次,在两个区域运动的轨迹如图,半径R1>R2,假定穿过铝板前后粒子电量保持不变,则该粒子( )
薄铝板将同一匀强磁场分成Ⅰ、Ⅱ两个区域,高速带电粒子可穿过铝板一次,在两个区域运动的轨迹如图,半径R1>R2,假定穿过铝板前后粒子电量保持不变,则该粒子( )
 薄铝板将同一匀强磁场分成Ⅰ、Ⅱ两个区域,高速带电粒子可穿过铝板一次,在两个区域运动的轨迹如图,半径R1>R2,假定穿过铝板前后粒子电量保持不变,则该粒子( )
薄铝板将同一匀强磁场分成Ⅰ、Ⅱ两个区域,高速带电粒子可穿过铝板一次,在两个区域运动的轨迹如图,半径R1>R2,假定穿过铝板前后粒子电量保持不变,则该粒子( )| A. | 带负电 | B. | 在Ⅰ、Ⅱ区域的运动速度相同 | ||
| C. | 在Ⅰ、Ⅱ区域的运动时间相同 | D. | 从区域Ⅰ穿过铝板运动到区域Ⅱ |
12.关于近代物理,下列说法正确的是( )
| A. | α射线是高速运动的氦原子 | |
| B. | 核聚变反应方程${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n中,${\;}_{0}^{1}$n表示质子 | |
| C. | 从金属表面逸出的光电子的最大初动能与照射光的频率不成正比 | |
| D. | 玻尔将量子观念引入原子领域,其理论能够解释氦原子光谱的特征 |
19.用比值法定义物理量是物理学中一种常用的方法,下面四个物理量都是用比值法定义的,其中定义式正确的是( )
| A. | 电容C=$\frac{Q}{U}$ | B. | 加速度a=$\frac{F}{m}$ | C. | 电场强度E=k$\frac{Q}{{r}^{2}}$ | D. | 电阻R=$\frac{U}{I}$ |
16.据媒体报道,嫦娥一号卫星环月工作轨道为圆轨道,卫星离月球表面的高度为200km,运行周期127min.若还知道引力常量G和月球平均半径R,仅利用上述条件能求出的是( )
| A. | 月球表面的重力加速度 | B. | 月球对卫星的引力 | ||
| C. | 卫星绕月球运行的速度 | D. | 卫星绕月球运行的加速度 |
17. 如图所示,一细束白光通过三棱镜折射后分为各种单色光,取其中a、b、c三种单色光,并同时做如下实验:①让这三种单色光分别通过同一双缝干涉装置在光屏上产生干涉条纹(双缝间距和缝屏间距不变);②让这三种单色光分别垂直投射到一条直光纤的端面上;下列说法中不正确的是( )
如图所示,一细束白光通过三棱镜折射后分为各种单色光,取其中a、b、c三种单色光,并同时做如下实验:①让这三种单色光分别通过同一双缝干涉装置在光屏上产生干涉条纹(双缝间距和缝屏间距不变);②让这三种单色光分别垂直投射到一条直光纤的端面上;下列说法中不正确的是( )
 如图所示,一细束白光通过三棱镜折射后分为各种单色光,取其中a、b、c三种单色光,并同时做如下实验:①让这三种单色光分别通过同一双缝干涉装置在光屏上产生干涉条纹(双缝间距和缝屏间距不变);②让这三种单色光分别垂直投射到一条直光纤的端面上;下列说法中不正确的是( )
如图所示,一细束白光通过三棱镜折射后分为各种单色光,取其中a、b、c三种单色光,并同时做如下实验:①让这三种单色光分别通过同一双缝干涉装置在光屏上产生干涉条纹(双缝间距和缝屏间距不变);②让这三种单色光分别垂直投射到一条直光纤的端面上;下列说法中不正确的是( )| A. | 如果单色光b不能产明显衍射,则单色光C也一定不能产生明显衍射 | |
| B. | 单色光c的波动性最显著 | |
| C. | 单色光a穿过光纤的时间最短 | |
| D. | 单色光c形成的干涉条纹间距最小 |
 如图所示,长为L,倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q,质量为m的小球,以初速度v0由斜面底端的A点开始沿斜面上滑,到达斜面顶端B的速度也为v0,求:
如图所示,长为L,倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q,质量为m的小球,以初速度v0由斜面底端的A点开始沿斜面上滑,到达斜面顶端B的速度也为v0,求: