题目内容
15.物理小组在一次探究活动中测量滑块与木板之间的动摩擦因数.实验装置如图甲所示,一表面粗糙的木板固定在水平桌面上,一端装有定滑轮:木板上有一滑块,其一端与穿过电磁打点计时器的纸带相连,另一端通过跨过定滑轮的细线与托盘连接.打点计时器使用的交流电源的频率为50Hz.开始实验时,在托盘中放入适 量砝码,滑块开始做匀加速运动,在纸带上打出一系列点.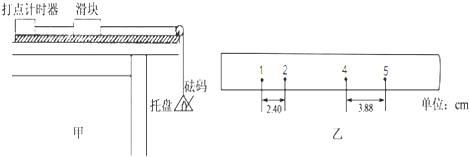
(1)图乙给出的是实验中获取的一条纸带的一部分:1、2、3、4、5是计数点,其中每相邻两计数点间还有4个计时点(图中未标出),测量出了1、2和4、5计数点间距离如图所示.根据图中数据计算的加速度a=0.49m/s2(保留两位有效数字).
(2)为了测量动摩擦因数,下列物理量中还应测量的是CD.
A.木板的长度L B.木板的质量m1C.滑块的质量m2D.托盘和砝码的总质量m3E.滑块运动的时间t
(3)滑块与木板间的动摩擦因数μ=$\frac{{m}_{3}g-({m}_{2}+{m}_{3})a}{{m}_{2}g}$(用被测物理量的字母表示,重力加速度为g).
分析 (1)利用逐差法△x=aT2可以求出物体的加速度大小,根据匀变速直线运动中某点的瞬时速度等于该过程中的平均速度大小可以求出某点的瞬时速度大小;
(2)根据牛顿第二定律有=ma,由此可知需要测量的物理量.
(3)根据牛顿第二定律的表达式,可以求出摩擦系数的表达式.
解答 解:(1)电源频率为50Hz,每相邻两计数点间还有4个计时点,则计数点间的时间间隔:t=0.02×5=0.1s,
由匀变速运动的推论△x=aT2可知:加速度a=$\frac{{x}_{6}-{x}_{3}}{3{t}^{2}}$=$\frac{0.0388-0.0240}{3×0.{1}^{2}}$≈0.49m/s2;
(2)以系统为研究对象,由牛顿第二定律得:
m3g-f=(m2+m3)a,滑动摩擦力:f=m2gμ,
解得:μ=$\frac{{m}_{3}g-({m}_{2}+{m}_{3})a}{{m}_{2}g}$,要测动摩擦因数μ,
需要测出:滑块的质量m2 与托盘和砝码的总质量m3,
故选:CD;
(3)由(2)可知,动摩擦因数的表达式为:μ=$\frac{{m}_{3}g-({m}_{2}+{m}_{3})a}{{m}_{2}g}$;
故答案为:(1)0.49;(2)CD;(3)$\frac{{m}_{3}g-({m}_{2}+{m}_{3})a}{{m}_{2}g}$.
点评 解决实验问题首先要掌握该实验原理,了解实验的操作步骤和数据处理以及注意事项,同时要熟练应用所学基本规律解决实验问题.

练习册系列答案
相关题目
6.以下关于电场和电场线的说法中正确的是( )
| A. | 同一试探电荷在电场线密集的地方所受电场力大 | |
| B. | 电场线不仅能在空间相交,也能相切 | |
| C. | 越靠近正点电荷,电场线越密,电场强度越大,越靠近负点电荷,电场线越稀,电场强度越小 | |
| D. | 电场线是人们假想的,用以表示电场的强弱和方向,和电场一样实际并不存在 |
6.有一条两岸平直、河水均匀流动、流速恒定的河流,小强驾着小船渡河,去程时行驶路线与河岸垂直,回程时船头指向始终与河岸垂直.去程与回程所用时间的比值为k,若船在静水中的速度大小为v,则河水流速为( )
| A. | $\frac{\sqrt{{k}^{2}-1}}{k}$v | B. | v$\sqrt{1-{k}^{2}}$ | C. | v$\sqrt{{k}^{2}+1}$ | D. | $\frac{\sqrt{1+{k}^{2}}}{k}$v |
10.关于科学家和他们的贡献,下列说法正确的是 ( )
| A. | 普朗克曾经大胆假设:振动着的带电微粒的能量只能是某一最小能量值ε的整数倍,这个不可再分的最小能量值ε叫做能量子 | |
| B. | 卢瑟福认为,原子是一个球体,正电荷弥漫性地均匀分布在整个球体内,电子镶嵌其中 | |
| C. | 按照爱因斯坦的理论,在光电效应中,金属中的电子吸收一个光子获得的能量是hν,这些能量的一部分用来克服金属的逸出功W0,剩下的表现为逸出后电子的初动能Ek | |
| D. | 玻尔的原子理论第一次将量子观念引入原子领域,提出了定态和跃迁的概念,成功地解释了所有原子光谱的实验规律 | |
| E. | 德布罗意提出:实物粒子也具有波动性,而且粒子的能量ε和动量p跟它对所应的波的频率ν和波长λ之间,遵从关系v=$\frac{?}{h}$和λ=$\frac{h}{p}$ |
20.下列说法正确的是 ( )
| A. | 康普顿效应说明光具有粒子性 | |
| B. | 居里夫人发现天然放射现象,揭示原子核内部有复杂的结构 | |
| C. | 一束光照射到某种金属上不能发生光电效应,是因为该束光的频率太小 | |
| D. | 将放射性元素掺杂到其他稳定元素中,并升高其温度,增加压强,它的半衰期也不会发生改变 | |
| E. | 碘131发生β衰变时所释放的电子是原子核内的质子转化为中子时产生的 |
4. 一列简谐横波在t=0时刻的波形如图所示,质点P此时刻沿-y方向运动,经过0.2s第一次回到平衡位置,则( )
一列简谐横波在t=0时刻的波形如图所示,质点P此时刻沿-y方向运动,经过0.2s第一次回到平衡位置,则( )
 一列简谐横波在t=0时刻的波形如图所示,质点P此时刻沿-y方向运动,经过0.2s第一次回到平衡位置,则( )
一列简谐横波在t=0时刻的波形如图所示,质点P此时刻沿-y方向运动,经过0.2s第一次回到平衡位置,则( )| A. | 该波沿x轴正方向传播 | B. | 波的周期为0.2s | ||
| C. | 波的传播速度为30m/s | D. | 质点Q的振动方程为y=5cos5πt(cm) |
5. 如图所示,理想变压器原线圈上连接着在水平面内的长直平行金属导轨,导轨之间存在垂直于导轨平面的匀强磁场,金属杆MN垂直放置在导轨上,且接触良好.移动变压器副线圈上的滑动触头可改变副线圈匝数,副线圈上接有一只理想电压表,滑动变阻器R的总阻值大于定值电阻R0的阻值,线圈L的直流电阻、导轨和金属杆的电阻都忽略不计.现在让金属杆以速度v=v0sin$\frac{2π}{T}$t的规律在导轨上左右来回运动,两灯A、B都发光.下列说法中不正确的是( )
如图所示,理想变压器原线圈上连接着在水平面内的长直平行金属导轨,导轨之间存在垂直于导轨平面的匀强磁场,金属杆MN垂直放置在导轨上,且接触良好.移动变压器副线圈上的滑动触头可改变副线圈匝数,副线圈上接有一只理想电压表,滑动变阻器R的总阻值大于定值电阻R0的阻值,线圈L的直流电阻、导轨和金属杆的电阻都忽略不计.现在让金属杆以速度v=v0sin$\frac{2π}{T}$t的规律在导轨上左右来回运动,两灯A、B都发光.下列说法中不正确的是( )
 如图所示,理想变压器原线圈上连接着在水平面内的长直平行金属导轨,导轨之间存在垂直于导轨平面的匀强磁场,金属杆MN垂直放置在导轨上,且接触良好.移动变压器副线圈上的滑动触头可改变副线圈匝数,副线圈上接有一只理想电压表,滑动变阻器R的总阻值大于定值电阻R0的阻值,线圈L的直流电阻、导轨和金属杆的电阻都忽略不计.现在让金属杆以速度v=v0sin$\frac{2π}{T}$t的规律在导轨上左右来回运动,两灯A、B都发光.下列说法中不正确的是( )
如图所示,理想变压器原线圈上连接着在水平面内的长直平行金属导轨,导轨之间存在垂直于导轨平面的匀强磁场,金属杆MN垂直放置在导轨上,且接触良好.移动变压器副线圈上的滑动触头可改变副线圈匝数,副线圈上接有一只理想电压表,滑动变阻器R的总阻值大于定值电阻R0的阻值,线圈L的直流电阻、导轨和金属杆的电阻都忽略不计.现在让金属杆以速度v=v0sin$\frac{2π}{T}$t的规律在导轨上左右来回运动,两灯A、B都发光.下列说法中不正确的是( )| A. | 只增大T,则灯A变暗、灯B变亮 | |
| B. | 当时间t=T时,两灯都亮着,电压表的示数为零 | |
| C. | 只将变阻器R的滑片下滑时,通过副线圈的电流减小,电压表的示数变大 | |
| D. | 只增大v0,两灯都变亮,杆MN来回运动的最大距离变小 |
 滑块A、B沿光滑水平面上同一条直线发生碰撞;碰撞后两者粘在一起运动;两者的位置x随时间t变化的图象如图所示.求:
滑块A、B沿光滑水平面上同一条直线发生碰撞;碰撞后两者粘在一起运动;两者的位置x随时间t变化的图象如图所示.求: